Los sistemas se usan para procesar una señal con el objetivo de modificarla, por ejemplo sumar o restar información adicional.
Un sistema puede considerarse como un proceso en el cual las señales de entrada son transformadas o modificadas y se obtienen nuevas señales a la salida del sistema.
Representación de sistemas
Un sistema para análisis y diseño es una representación de un proceso físico, que relaciona las señales de entrada $x(t)$ y las señales de salida $y(t)$ obtenidas como respuesta.
La representación puede ser de tipo matemática o en diagramas de bloques con flechas. El sentido de las flechas indican la entrada o salida.
Los sistemas se pueden realizar por: – Componentes físicos (hardware: componentes electrónicos) – Algoritmos (software: calculan la nueva señal a partir de la entrada)
Sistemas Contínuos
En un sistema contínuo las señales contínuas de entrada son transformadas en señales contínuas de salida.
$$\large x(t) \rightarrow y(t)$$

Ejemplo: Un sistema de transmision A.M o transmision F.M
Sistemas Discretos
Cuando las entradas de tiempo discreto se transforman en en salidas de tiempo discreto, al sistema se denomina «sistema discreto».
$$\large x[n] \rightarrow y[n]$$

Ejemplo: Sistema de transmision de datos de una computadora
Entradas y salidas de un sistema
Los sistemas pueden tener.
– Una entrada y una salida (SISO – Single Input, Single output) – Varias entradas, varias salidas (MIMO – Multiple Input, Multiple output)
Un sistema puede estar compuesto de subsistemas interconectados, caracterizados por sus terminales de entrada y salida.
Interconexion de Sistemas
Los sistemas pueden crearse a partir de subsistemas más sencillos. La interconexion entre los sistemas permite resolver problemas de mayor complejidad.
La interconexión de dos sistemas puede ser realizada de tres maneras:
- Interconexión en serie (cascada)
- Interconexión en paralelo
- Interconexión en serie-paralelo
- Interconexión con retroalimentación.
Para ilustrar las formas de interconexión de forma gráfica se usan los diagramas de bloques, al interconectar las salidas y entradas entre bloques.
Inteconexión en serie
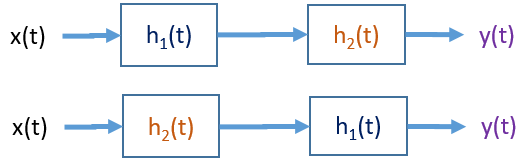
Los subsistemas se conectan secuencialmente usando la salida a una entrada.
Ejemplo: la salida de video de la computadora hacia la entrada de video del proyector en el aula de clases, usada para proyectar el contenido del curso.
Inteconexión en Paralelo
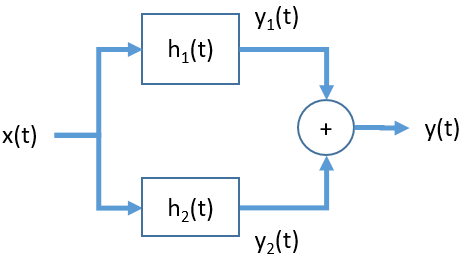
La señal de entrada se aplica simultaneamente o en paralelo a dos los subsistemas, el símbolo ‘+’ expresa que el resultado es la suma de los resultados de los sistemas 1 y 2.
Ejemplo: un sistema de mezcla de sonido proveniente de varios microfonos e instrumentos musicales.
Interconexión serie-paralelo
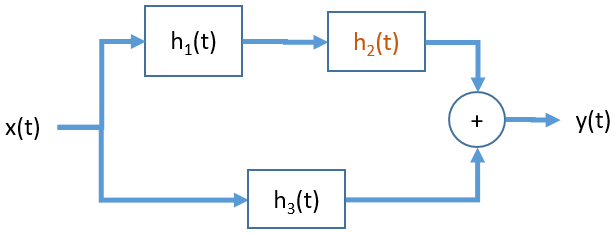
Estos sistemas son una combinacion de sistemas en serie y paralelo, La mayoria de sistemas son del tipo serie-paralelo.
Interconexión con retroalimentación
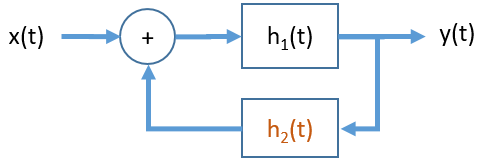
Los sistemas retroalimentados permiten «regular» la salida «observando una parte de la misma.
Ejemplo: El sistema de control de potencia de transmision en un celular, El motor de un ascensor, etc.
Propiedades de los Sistemas
- Memoria
- Invertibilidad
- Estabilidad
- Causalidad
- Invarianza en el tiempo
- Linealidad
Memoria
Si la salida de un sistema depende solo del valor aplicado en la entrada actualmente, se dice que el sistema es sin memoria.
$$ \large y[n] = (x[n]^2- 4x[n] )^3 $$
Si el sistema depende de los valores anteriores de la entrada, se lo considera con memoria.
$$ \large y[n]= x[n-1] +2x[n-3]$$
Los sistemas sin memoria también se conocen como instantaneos, que son un caso particular de los sistemas dinámicos (con memoria).
Un sistema cuya respuesta en $t$ está determinada por los anteriores $T$ segundos, es decir el intervalo $(t–T)$, se lo conoce como «sistema con memoria finita»
Invertibilidad
Un sistema es invertible si entradas distintas producen salidas distintas.
Dada una salida, es posible deducir la entrada que la provocó.(Biyectiva).
Para un sistema invertible hay un sistema inverso que, conectado en cascada con aquél, produce una salida igual a su entrada.
$$ \large y(t)= 2x(t) \rightarrow x(t) = \frac{1}{2}y(t)$$
$$\large y(t)= x(t)^2$$
Estabilidad
Un sistema es estable si para una entrada de valor limitado la salida también es limitada y no diverge. En otras palabras, si el sistema tiene como entrada un valor finito la salida debe ser finita para que exista estabilidad, los sistemas inestables tienen una entrada finita y su salida se vuelve muy grande tendiendo a infinito.
Causalidad
Un sistema es CAUSAL (no-anticipativo o físico) si la salida $y(t)$ en un valor arbitrario de tiempo $t=t_0$ depende solo de la entrada $x(t)$ para $t ≤ t_0$ , es decir depende solo de los valores presentes y/o pasados de la entrada; no depende de valores futuros.
No es posible obtener una salida antes que se aplique la entrada.
$$ \large y(t) = x(t - 1)$$
si $t$ es en segundos, la salida depende de los valores de $x$ hace un segundo o $(t-1)$
En el caso contrario, los sistemas NO CAUSALES muestran una salida anticipada a la señal de entrada:
$$\large y(t) = x(t + 1)$$
si $t$ es en segundos, la salida depende de los valores que $x$ tendría un segundo después o $(t+1)$. Si $t$ es en días, la situación se vuelve complicada de realizar, es como decir: para determinar el valor de la variable $y(t)$ HOY, necesitamos conocer el valor de $x(t+1)$ que es MAÑANA.
Los sistemas no-casuales por tener variable independiente referenciada a tiempo futuro, no se pueden implementar en tiempo real. Sin embargo si los sistemas no causales se realizan con variables diferentes al tiempo, por ejemplo espacio se podrían implementar.
Invarianza en el tiempo
Si el comportamiento de un sistema y las características del mismo están fijos en el tiempo, se los llama invariantes en el tiempo.
Expresando lo mismo como: Un sistema es Invariante en el tiempo si aun corrimiento de tiempo en la señal de entrada ocasiona un corrimiento en el tiempo en la señal de salida.
$$ \large y(t) = x(t) \ y(t-t_0) = x(t-t_0)$$
Ejemplo (Oppenheim 1.14):
considere un sistema definido como:
$$\large y(t) = \sin(x(t)) \text{, siendo x(t)=t} $$ $$\large y(t-t_0) = \sin(x(t - t_0)) $$
# Importar librerias basicas
import numpy as np
import matplotlib.pyplot as plt
import sympy as sym
%matplotlib inline
plt.style.use('bmh') # estilo de las graficas
from IPython.display import Latex # para visualizar ecuaciones en jupyter
# Sistemas – Invariantes en el tiempo
# Oppenheim 1.14
import numpy as np
# INGRESO
a = 0; b = 2*np.pi ; dt=0.1
t0 = 1
xt = lambda t: t
yt = lambda t: np.sin(xt(t))
# PROCEDIMIENTO
t = np.arange(a,b,dt)
x1 = xt(t)
y1 = yt(t)
# Corrimiento en la entrada
t2x = t + t0
x2 = x1
# efecto en salida
t2y = t + t0
y2 = y1
# evaluación de tiempos desplazados
y3 = yt(t-t0)
# SALIDA - GRAFICA
import matplotlib.pyplot as plt
plt.figure(figsize=(10,5))
plt.plot(t,y1, label='y1(t)')
plt.plot(t2y,y2, 'm.', label='y2(t)')
plt.plot(t,y3, label='y1(t-t0)')
plt.xlabel('t')
plt.legend()
plt.show()
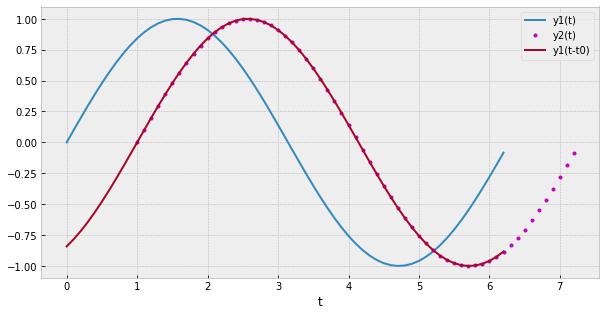
Por otro lado, si la respuesta de la señal se modifica en el tiempo, el sistema será VARIANTE en el tiempo:
Ejemplo (Oppenheim 1.14):
Considere el sistema: $$\large y(t) = x(2t)$$
que tiene escalamiento en el tiempo. $y(t)$ es una versión comprimida de $x(t)$. Los corrimientos/desplazamientos en el tiempo también serán comprimidos por un factor de 2, por lo que por ésta razón el sistema no es invariante en el tiempo.
# Sistemas – Invariantes en el tiempo
# Oppenheim 1.16 p52/pdf80
import numpy as np
# INGRESO
a = -5; b = 5 ; dt=0.1
t0 = 2
u = lambda t: np.piecewise(t,t>=0,[1,0])
xt = lambda t: u(t+2)-u(t-2)
yt = lambda t: xt(2*t)
# PROCEDIMIENTO
t = np.arange(a,b,dt)
x1 = xt(t)
y1 = yt(t)
# Corrimiento en la entrada
t2x = t + t0
x2 = x1
# efecto compresor en salida
t2y = t + t0/2
y2 = y1
# evaluación de tiempos desplazados
x3 = xt(t-t0)
y3 = yt(t-t0)
# SALIDA - GRAFICA
import matplotlib.pyplot as plt
plt.figure(figsize=(10,6))
plt.subplot(311)
plt.xlim([min(t),max(t)])
plt.plot(t,x1, label='x1(t)')
plt.plot(t,y1, label='y1(t)')
plt.legend()
plt.subplot(312)
plt.xlim([min(t),max(t)])
plt.plot(t2x,x2, label='x2(t)=x1(t-t0)')
plt.plot(t2y,y2, label='y2(t)')
plt.legend()
plt.subplot(313)
plt.xlim([min(t),max(t)])
plt.plot(t,y3,color ='orange', label='y1(t-t0)')
plt.xlabel('t')
plt.legend()
plt.show()
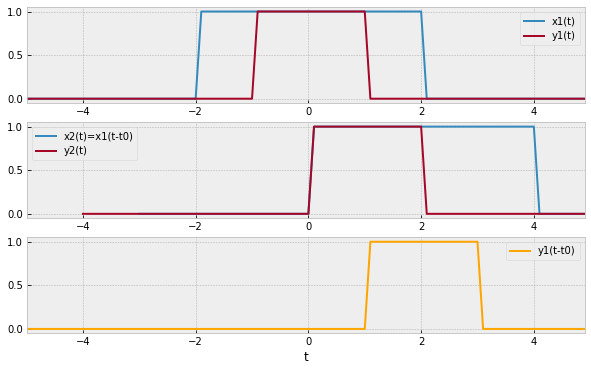
El sistema tiene una relación de entrada-salida dada por:
$\large y(t) = x(2t)$ y $\large t_0$ es un desplazamiento en el tiempo.
Sea $\large y_2(t)$ la respuesta a $\large x_2(t) = x(t-t_0)$ entonces:
$\large y_2(t) = x_2(2t) = x(2t-t_0)$
$\large y(t-t_0) = x(2(t-t_0))$
$\large y(t-t0) \neq y_2(t)$, por lo que el sistema no es invariante en el tiempo. El sistema $\large x(2t)$ se conoce como compresor, pues crea una secuencia de salida cada 2 valores de la secuencia de entrada.
Linealidad
Un sistema es lineal si satisface el principio de superposición, que engloba las propiedades de escalado (homogeneidad) y aditividad.
En un sistema lineal tiene salida proporcional a su entrada y si la entrada es cero la salida debe ser cero.
Un sistema lineal tiene la propiedad de aditividad, es decir, la respuesta a una suma de señales en la entrada es igual a la suma de las entradas individuales.
- La respuesta a: $\large x_1(t) + x_2(t) = y_1(t) + y_2(t)$
- La respuesta a: $\large \alpha x1(t)$ es $\large \alpha y1(t)$, donde $\large \alpha$ es una constante real o compleja cualquiera.
El numeral 2 se conoce como la propiedad de escalamiento u homogeneidad.
La propiedad de Superposición se plantea como una combinación de las propiedades anteriores, osea que cumpla Aditividad y Homogeneidad:
en tiempo contínuo: $$\large \alpha x_1(t) + \beta x_2(t) → \alpha y_1(t) + \beta y_2(t)$$ en tiempo discreto: $$\large \alpha x_1[n] + \beta x_2[n] → \alpha y_1[n] + \beta y_2[n]$$
En el curso nos enfocaremos principalmente en los sistemas Lineales e invariantes en el tiempo, que son llamados Sistemas LTI (Linear Time Invariance)
REFERENCIAS
- Oppenheim 1.5
- Oppenheim 1.5.2
- Oppenheim 1.6.1
- Oppenheim 1.6.3
- Oppenheim 1.6.5
- Oppenheim 1.6.6
- http://enrique.sanchez.webs.uvigo.es/PDFs/125_TemaI-Senales.pdf
- http://blog.espol.edu.ec/telg1001/sistemas/
Phd. Jose R. Zapata
