# Importar librerias basicas
import numpy as np
import matplotlib.pyplot as plt
import sympy as sym
%matplotlib inline
plt.style.use('bmh') # estilo de las graficas
from IPython.display import Latex # para visualizar ecuaciones en jupyter
Función de Transferencia
En el dominio del tiempo se utilizan diferentes representaciones para caracterizar los sistemas lineales invariantes en el tiempo (LTI). Por ejemplo, los coeficientes constantes de ecuaciones diferenciales parciales ordinarias (EDO), la respuesta al impulso y la respuesta a paso. La función de transferencia denota el factor complejo $H(s)$, sobre la función propia $e^{s t}$ en la entrada de un sistema LTI y se pondera cuando pasa por el sistema. Dado que la transformada de Laplace descompone señales con respecto a estas funciones propias, la función de transferencia constituye una representación de un sistema LTI en el dominio espectral (Laplace o Fourier). Los enlaces entre la función de transferencia y las representaciones en el dominio del tiempo de los sistemas LTI se analizan en este capitulo.
Relación con la respuesta al impulso y las señales de entrada / salida
Ya se describió en el contexto del teorema de convolución de Fourier y la transformada de Laplace, que un sistema LTI puede representarse de manera equivalente en el dominio del tiempo y en el dominio de la frecuencia (espectro). En el dominio del tiempo, la salida $y(t)$ de un sistema LTI se da al convolucionar la señal de entrada $x(t)$ con la respuesta de impulso $h(t)$ de sistema
$$ y(t) = x(t) * h(t) $$
Aplicando el teorema de convolución de la transformada de Laplace produce
$$ Y(s) = X(s) \cdot H(s) $$
donde $X(s) = \mathcal{L} { x(t) }$ y $Y(s) = \mathcal{L} { y(t) }$ son las transformadas de Laplace de la señal de entrada y salida, respectivamente. La función de transferencia $H(s)$ se da como la transformada de Laplace de la respuesta al impulso $h(t)$
$$ H(s) = \mathcal{L} { h(t) } $$
Esto también se puede concluir a partir de la relacion entre la respuesta al impulso y la función de transferencia. Los resultados derivados muestran que un sistema LTI se puede caracterizar completamente en el dominio del tiempo y de la frecuencia por su respuesta al impulso $h(t)$ o la función de transferencia $H(s)$ o la respuesta en frecuencia $H(j \omega)$, respectivamente.
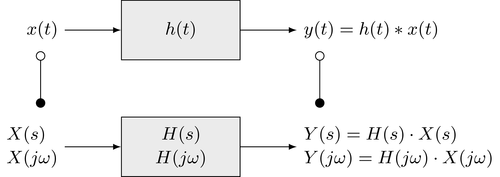
Además, se puede concluir que la función de transferencia se da como el cociente entre la salida $Y(s)$ y la señal de entrada $X(s)$ en el dominio de Laplace
$$ H(s) = \frac{Y(s)}{X(s)} $$
para $X(s) \neq 0$. Las mismas relaciones se mantienen en el dominio de Fourier si la región de convergencia (ROC) de la respuesta al impulso incluye el eje imaginario $\Re { s } = 0$. En general, la función de transferencia puede derivarse mediante la división de los espectros de la señal de salida y entrada. Esto se puede utilizar para medir la función de transferencia de un sistema mediante señales de entrada específicas que cumplen con $X(s) \neq 0$ con $X(s) \approx$ constante.
Ejemplo
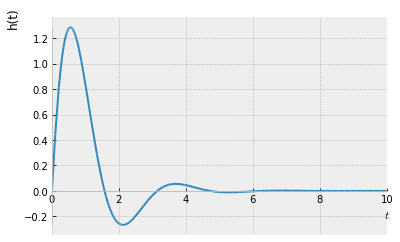
La función de transferencia $H(s)$ de un filtro pasa bajos de segundo orden es:
$$ H(s) = \frac{1}{C L s^2 + C R s + 1} $$
la respuesta al impulso $h(t)$ del paso bajo está dada por la transformada inversa de Laplace de la función de transferencia $H(s)$. Primero, la función de transferencia se define en SymPy
import sympy as sym
%matplotlib inline
sym.init_printing()
R, L, C = sym.symbols('R L C', positive=True)
s = sym.symbols('s', complex=True)
H = 1/(C*L*s**2 + C*R*s + 1)
H
$\displaystyle \frac{1}{C L s^{2} + C R s + 1}$
Luego, la transformada inversa de Laplace se calcula para los valores normalizados específicos $L = .5$, $R = 1$, $C = .4$ de los elementos del circuito.
t = sym.symbols('t', real=True)
RLC = {R: 1, L: sym.Rational('.5'), C: sym.Rational('.4')}
h = sym.inverse_laplace_transform(H.subs(RLC), s, t)
h
$\displaystyle \frac{5 e^{- t} \sin{\left(2 t \right)} \theta\left(t\right)}{2}$
Se grafican los resultados
sym.plot(h, (t, 0, 10), xlabel='$t$', ylabel='h(t)');
Relacion con las ecuaciones Diferenciales de Coeficientes Constantes
Como se habia encontrado anteriormente la función de transferencia $H(s)$ del sistema como
$$ H(s) = \frac{Y(s)}{X(s)} = \frac{\sum_{m=0}^{M} \beta_m s^m}{\sum_{n=0}^{N} \alpha_n s^n} $$
La función de transferencia de un sistema LTI cuya relación de entrada y salida puede caracterizarse por una ecuación diferencial de coeficientes constantes se da como función racional en $s$. Los coeficientes de su polinomio numerador y denominador están dados por los coeficientes $\beta_m$ y $\alpha_n$ de la ecuación diferencial. La conversión entre ambas representaciones de un sistema LTI es, por lo tanto, sencilla.
Ejemplo
Los coeficientes para el filtro pasa bajos de segundo orden se pueden determinar a partir de la ecuaicon diferencial de coeficientes constantes o desde la función de transferencia anterior como
$$ \begin{align} \beta_0 &= 1 & \alpha_0 &= 1 \ & & \alpha_1 &= C R \ & & \alpha_2 &= C L \end{align} $$
A partir de estos coeficientes, la función de transferencia $H(s)$ se construye en SymPy
R, L, C = sym.symbols('R L C', positive=True)
beta = 1
alpha = L*C, R*C, 1
H = sym.Poly(beta, s) / sym.Poly(alpha, s)
H
$\displaystyle \frac{1}{C L s^{2} + C R s + 1}$
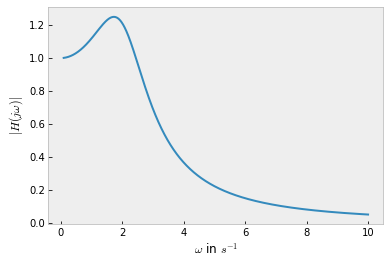
Muchos paquetes de software para procesamiento de señales tienen la funcionalidad para el cálculo de la función de transferencia desde los coeficientes $\beta_m$ y $\alpha_n$ de un sistema. Por ejemplo, la caja de herramientas de procesamiento de señal de Python scipy.signal proporciona una función para evaluar numéricamente la función de transferencia $H(j \omega)$ en un número de frecuencias angulares $\omega_i$ para un conjunto dado de coeficientes. Esto se ilustra a continuación para los valores normalizados $R$, $L$ y $C$ utilizados anteriormente.
from scipy import signal
R = 1
L = 0.5
C = 0.4
beta = 1
alpha = L*C, R*C, 1
w, H = signal.freqresp((beta, alpha))
Esto da como resultado el vector w de frecuencias angulares discretas $\omega_i$ y el vector H con los valores de $H(j \omega)$ en estas frecuencias.
import matplotlib.pyplot as plt
plt.plot(w, abs(H))
plt.xlabel('$\omega$ in $s^{-1}$')
plt.ylabel('$|H(j \omega)|$')
plt.grid();
Diagramas de BODE
La función de la respuesta en freuencia Fourier $H(j \omega)$ caracteriza las propiedades de transmisión de un sistema (LTI) con respecto a una señal exponencial armónica $e^{j \omega t}$ con frecuencia angular $\omega = 2 \pi f$. Para ilustrar las características de un sistema LTI, a menudo la magnitud $| H(j \omega) |$ y la fase $\varphi_H(j \omega)$ de la función de transferencia se consideran por separado. Descomponiendo la señal de salida $Y(j \omega) = X(j \omega) \cdot H(j \omega)$ en su magnitud $| Y(j \omega) |$ y la grafica de fase $\varphi_Y(j \omega)$
\begin{align} | Y(j \omega) | &= | X(j \omega) | \cdot | H(j \omega) | \ \varphi_Y(j \omega) &= \varphi_X(j \omega) + \varphi_H(j \omega) \end{align}
donde $X(j \omega)$ denota la señal de entrada, y $| X(j \omega) |$ y $\varphi_X(j \omega)$ su magnitud y fase, respectivamente. Se puede concluir de las ecuaciones anteriores, que la magnitud $| H(j \omega) |$ proporciona la atenuación dependiente de la frecuencia de la magnitud $| X(j \omega) |$ de la señal de entrada por el sistema, mientras que $\varphi_H(j \omega)$ proporciona el cambio de fase introducido.
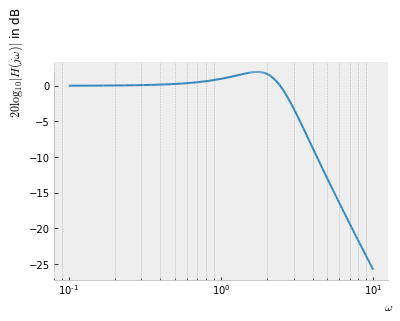
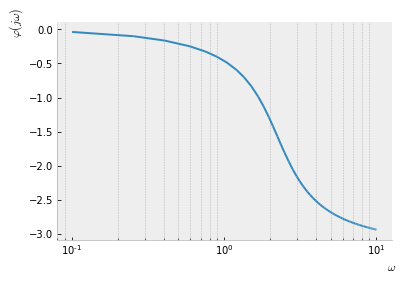
Una ilustración gráfica de uso común de las propiedades del sistema en términos de magnitud y fase de la función de transferencia son los diagramas de Bode. Aquí la magnitud logarítmica de la función de transferencia $20 \log_{10} | H(j \omega) |$ en decibelios se grafica contra el logaritmo de la frecuencia $\omega$ o $f$. La fase $\varphi_H(j \omega)$ se grafica linealmente contra el logaritmo de la frecuencia.
%matplotlib inline
sym.init_printing()
s = sym.symbols('s')
w = sym.symbols('omega', real=True)
R, L, C = sym.symbols('R L C', positive=True)
H = 1/(C*L*s**2 + C*R*s + 1)
H = H.subs(s, sym.I * w)
H
$\displaystyle \frac{1}{- C L \omega^{2} + i C R \omega + 1}$
El diagrama de bode se genera para los valores normalizados $R = 1$, $L = 0.5$ y $C = 0.4$
from sympy.plotting.plot import MatplotlibBackend
def logx_plot(Hw, wrange, **kwargs):
'create plot with logarithmic x-axis'
p = sym.plot(Hw, wrange, show=False, **kwargs)
backend = MatplotlibBackend(p)
backend.process_series()
backend.ax.spines['left'].set_position(('axes', 0))
backend.ax.spines['bottom'].set_position(('axes', 0))
plt.xscale('log')
plt.grid(which='both')
def db(x):
'compute dB value'
return 20 * sym.log(sym.Abs(x), 10)
RLC = {R: 1, L: sym.Rational('.5'), C: sym.Rational('.4')}
logx_plot(db(H.subs(RLC)), (w, 0.1, 10),
xlabel='$\omega$', ylabel='$20 \log_{10} | H(j \omega) |$ in dB')
logx_plot(sym.arg(H.subs(RLC)), (w, 0.1, 10),
xlabel='$\omega$', ylabel=r'$\varphi(j \omega)$')
Retraso de Fase y de Grupo (Phase and Group Delay)
El retraso de fase y grupo caracterizan las propiedades de fase y retraso de un sistema LTI. Ambos cuantifican el retraso dependiente de la frecuencia que se imprime en una señal cuando pasa a través de un sistema. En muchas aplicaciones, el retraso introducido por un sistema debe ser lo más pequeño posible o dentro de límites razonables.
Retraso de Fase
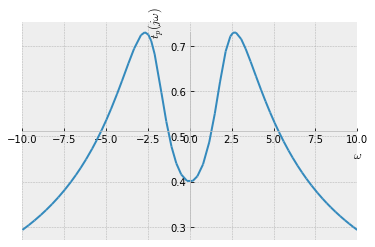
Para un sistema LTI con función de transferencia $H(j \omega)$, el retardo de fase se define de la siguiente manera
$$ t_p(\omega) = - \frac{\varphi(j \omega)}{\omega} $$
donde $\varphi(j \omega) = \arg { H(j \omega) }$ denota la fase de la función de transferencia. El retardo de fase cuantifica el retraso de una señal exponencial armónica única $e^{j \omega t}$ con frecuencia $\omega$ cuando pasa a través del sistema. El signo negativo en la definición del retraso de fase resulta en un retraso de fase positivo $t_p(\omega) > 0$ cuando un sistema retrasa una señal. Tenga en cuenta que el retraso de fase no esta definido para $\omega = 0$.
Como ejemplo, el retardo de fase $t_p(\omega)$ se calcula para el filtro de paso bajo de segundo orden. Primero, la función de transferencia $H(j \omega)$ se define en SymPy
%matplotlib inline
import sympy as sym
sym.init_printing()
L, R, C = sym.symbols('L R C', positive=True)
w = sym.symbols('omega', real=True)
s = sym.I * w
H = 1 / (C*L*s**2 + C*R*s + 1)
H
$\displaystyle \frac{1}{- C L \omega^{2} + i C R \omega + 1}$
Ahora se calcula el retraso de fase $t_p(\omega)$
phi = sym.arg(H)
tp = - phi/w
tp
$\displaystyle - \frac{\arg{\left(\frac{1}{- C L \omega^{2} + i C R \omega + 1} \right)}}{\omega}$
y el resultado se visualiza utilizando los valores normalizados $R=1$, $L=0.5$ y $C=0.4$ para los elementos del filtro de paso bajo
RLC = {R: 1, L: sym.Rational('.5'), C: sym.Rational('.4')}
sym.plot(tp.subs(RLC), (w, -10, 10),
xlabel='$\omega$', ylabel='$t_p(j \omega)$');
Retraso de Grupo
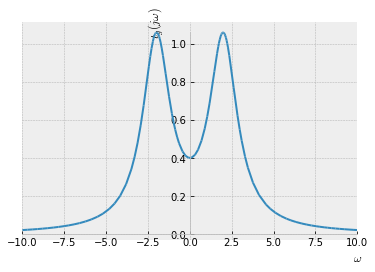
El retraso de grupo se define como la derivada de la fase con respecto a la frecuencia
$$ t_g(\omega) = - \frac{d \varphi(j \omega)}{d \omega} $$
El retraso de grupo cuantifica el retraso que observa la envolvente de amplitud de un grupo de señales exponenciales cuando pasa a través de un sistema. El signo negativo en la definición anterior da como resultado un retraso de grupo positivo para un sistema que impone un retraso en la señal de entrada. Tenga en cuenta que la fase $\varphi(j \omega)$ en general solo es única para $- \pi < \varphi(j \omega) \leq \pi$. Si la fase excede este rango, se envuelve. Para obtener resultados significativos, se requiere desenvolver la fase antes de calcular el retraso del grupo.
Ejemplo
El Retardo de grupo $t_g(\omega)$ del filtro de paso bajo de segundo orden anterior se calcula y se representa gráficamente para los valores normalizados
tg = - sym.diff(phi, w)
sym.plot(tg.subs(RLC), (w, -10, 10),
xlabel='$\omega$', ylabel='$t_g(j \omega)$');
Combinacion de Sistemas
Sistemas en Serie
Cuando dos sistemas lineales invariantes en el tiempo (LTI) se combinan en serie conectando la salida del primer sistema a la entrada de un segundo sistema, esto se denomina concatenación de dos sistemas o sistemas en serie. Denotando las respuestas de impulso de los dos sistemas por $h_1(t)$ y $h_2(t)$, la señal de salida $y(t)$ del segundo sistema se da como
$$ y(t) = x(t) * h_1(t) * h_2(t) $$
donde $x(t)$ denota la señal de entrada del primer sistema. La transformación de Laplace de las respectivas señales y respuestas de impulso, y la aplicación repetida del teorema de convolución produce
$$ Y(s) = \underbrace{H_1(s) \cdot H_2(s)}_{H(s)} \cdot X(s) $$
Se puede concluir que la concatenación de dos sistemas puede considerarse como un sistema LTI con la función de transferencia $H(s) = H_1(s) \cdot H_2(s)$. Por lo tanto, las siguientes estructuras son equivalentes
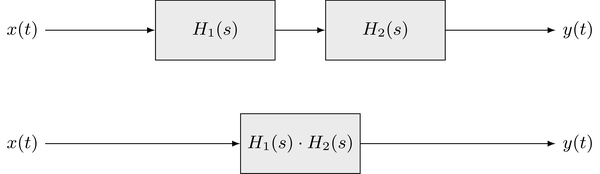
La extensión a una concatenación de sistemas $N$ es sencilla. La función de transferencia general viene dada por la multiplicación de todas las funciones de transferencia individuales $H_n(s)$
$$ H(s) = \prod_{n=1}^{N} H_n(s) $$
Las aplicaciones de los sistemas concatenados incluyen, por ejemplo, el modelado de sistemas de transmisión inalámbrica y filtros en cascada.
Ejemplo
La concatenación de sistemas LTI puede usarse para construir filtros de orden superior a partir de prototipos de orden inferior. Dichos filtros se conocen como filtros en cascada. La función de transferencia $H_0(s)$ del paso bajo se da como
$$ H_0(s) = \frac{1}{LC s^2 + RC s + 1} $$
donde $R$, $L$ y $C$ denotan los valores de la resistencia, el condensador y el inductor. La concatenación de los filtros de segundo orden $N$ conduce a un filtro con el orden $2 N$. Su función de transferencia se lee
$$ H_N(s) = \left( \frac{1}{LC s^2 + RC s + 1} \right)^N $$
La función de transferencia resultante se ilustra mediante su diagrama de Bode para un número variable de filtros en cascada utilizando los valores normalizados $L = .5$, $R = 1$, $C = .4$ . Primero se define la función de transferencia $H_N(s)$
%matplotlib inline
import sympy as sym
sym.init_printing()
s = sym.symbols('s', complex=True)
w, R, L, C = sym.symbols('omega R L C', real=True)
N = sym.symbols('N', integer=True)
H0 = 1/(L*C*s**2 + R*C*s + 1)
HN = H0**N
HN
$\displaystyle \left(C L s^{2} + C R s + 1\right)^{- N}$
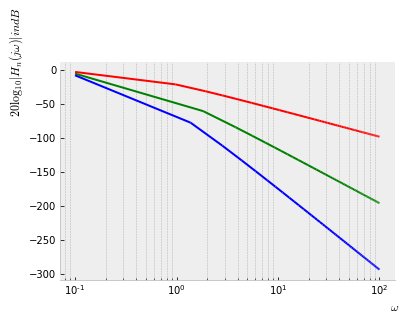
El diagrama de bode para la función de transferencia $H_N(j \omega)$ se muestra para $N = {1, 2, 3}$ (línea roja, verde, azul)
import matplotlib.pyplot as plt
from sympy.plotting.plot import MatplotlibBackend
RLC = {R: 1, L: sym.Rational('.5'), C: sym.Rational('.4')}
HNlog = 20*sym.log(sym.Abs(HN.subs(RLC).subs(s, 2*sym.pi*w)), 10)
p1 = sym.plot(HNlog.subs(N, 1), (w, 0.1, 100), xlabel='$\omega$', ylabel='$20 \log_{10} | H_n(j \omega) | in dB$', line_color='r', show=False);
p2 = sym.plot(HNlog.subs(N, 2), (w, 0.1, 100), xlabel='$\omega$', ylabel='$20 \log_{10} | H_n(j \omega) | in dB$', line_color='g', show=False);
p3 = sym.plot(HNlog.subs(N, 3), (w, 0.1, 100), xlabel='$\omega$', ylabel='$20 \log_{10} | H_n(j \omega) | in dB$', line_color='b', show=False);
p1.extend(p2)
p1.extend(p3)
backend = MatplotlibBackend(p1)
backend.process_series()
backend.ax.spines['left'].set_position(('axes', 0))
backend.ax.spines['bottom'].set_position(('axes', 0))
plt.xscale('log')
plt.grid(which='both')
Sistemas en Paralelo
Una estructura donde dos sistemas LTI comparten la misma señal de entrada y las señales de salida se superponen se llama conexión en paralelo. La señal de salida general $y(t)$ se da como la superposición de las señales de salida de los sistemas individuales
$$ y(t) = h_1(t) * x(t) + h_2(t) * x(t) $$
La Transformación de Laplace de las respectivas señales y respuestas de impulso, y la aplicación del teorema de convolución produce
$$ Y(s) = \underbrace{\left( H_1(s) + H_2(s) \right)}_{H(s)} \cdot X(s) $$
La función de transferencia global $H(s)$ de una conexión paralela de dos sistemas se da como la superposición de las funciones de transferencia de los sistemas individuales. Por lo tanto, las siguientes estructuras son equivalentes
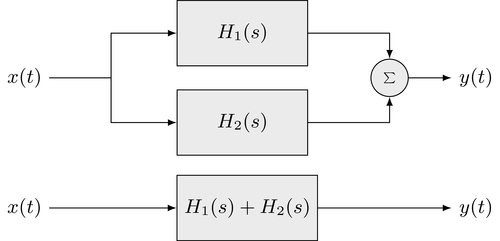
La extensión a una conexión paralela de sistemas $N$ es sencilla. La función de transferencia general viene dada por la superposición de todas las funciones de transferencia individuales $H_n(s)$
\begin{equation} H(s) = \sum_{n=1}^{N} H_n(s) \end{equation}
Una aplicación destacada de una conexión paralela de sistemas son bancos de filtros como se utilizan en el análisis de señales y muchos esquemas de codificación con pérdida como MP3, AAC, etc.
Sistema Realimentado
La conexión de dos sistemas LTI, donde la entrada del segundo sistema está conectada a la salida del primero y la salida del segundo sistema se superpone a la entrada del primero se llama circuito realimentado. Esta estructura se representa en la siguiente ilustración
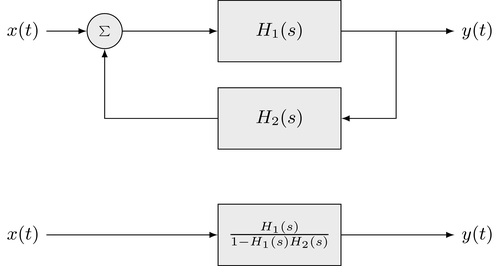
La señal de salida $y(t)$ se da como
$$ y(t) = x(t) * h_1(t) + y(t) * h_2(t) * h_1(t) $$
La transformada de Laplace de las señales y las respuestas a los impulsos, la aplicación del teorema de convolución y la reordenación de los rendimientos de los términos
$$ Y(s) = \frac{H_1(s)}{1 - H_1(s) \cdot H_2(s)} \cdot X(s) $$
La función de transferencia general $H(s)$ del ciclo de realimentación se da como
$$ H(s) = \frac{H_1(s)}{1 - H_1(s) \cdot H_2(s)} $$
Esta equivalencia se representa en el diagrama de bloques inferior de la estructura anterior.
Las aplicaciones de los circuitos de retroalimentación incluyen sistemas de control, diseño de amplificadores, entre otros.
REFERENCIAS
- https://nbviewer.jupyter.org/github/spatialaudio/signals-and-systems-lecture/blob/master/systems_spectral_domain/transfer_function.ipynb
- https://nbviewer.jupyter.org/github/spatialaudio/signals-and-systems-lecture/blob/master/systems_spectral_domain/bode_plot.ipynb
- https://nbviewer.jupyter.org/github/spatialaudio/signals-and-systems-lecture/blob/master/systems_spectral_domain/phase_group_delay.ipynb
- https://nbviewer.jupyter.org/github/spatialaudio/signals-and-systems-lecture/blob/master/systems_spectral_domain/combination.ipynb
Phd. Jose R. Zapata
