Representacion En la frecuencia de Señales Periodicas Mediante Series De Fourier
Las series de Fourier constituyen la herramienta matemática básica del análisis de Fourier empleado para analizar funciones periódicas a través de la descomposición de dicha función en una suma infinita de funciones senoidales mucho más simples (como combinación de senos y cosenos con frecuencias enteras). El nombre se debe al matemático francés Jean-Baptiste Joseph Fourier que desarrolló la teoría cuando estudiaba la ecuación del calor. Fue el primero que estudió tales series sistemáticamente, y publicando sus resultados iniciales en 1807 y 1811. Esta área de investigación se llama algunas veces Análisis armónico.
Es una aplicación usada en muchas ramas de la ingeniería, además de ser una herramienta sumamente útil en la teoría matemática abstracta. Áreas de aplicación incluyen análisis vibratorio, acústica, óptica, procesamiento de imágenes y señales, y compresión de datos. En ingeniería, para el caso de los sistemas de telecomunicaciones, y a través del uso de los componentes espectrales de frecuencia de una señal dada, se puede optimizar el diseño de un sistema para la señal portadora del mismo. Refierase al uso de un analizador de espectros.
Respuesta de los Sistemas LTI ante Exponenciales Complejas
En los sistemas LTI es importante poder representar señales como la combinacion lineal de señales basicas que posean 2 propiedades:
- El conjunto de señales basicas se puede usar para construir una amplia y util clase de señales
- La respuesta de un sistema LTI a cada una de las señales debe ser lo bastante sencilla en estructura como para proporcionarnos una representacion conveniente de la respuesta del sistema a cualquier señal construida como una combinacion lineal de señales basicas.
La respuesta de una sistema LTI antes una señal Exponencial Compleja es la misma señal Exponencial Compleja con un cambio de amplitud $$\large e^{st} \rightarrow H(s)e^{st} $$ $$\large Z^n \rightarrow H[z] Z^{n} $$
Donde $\large H(s)$ y $\large H[z]$ con los valores propios (eingen valores) y $\large e^{st}$ y $\large Z^{n}$ son las funciones propias (eingen funciones)
Esto se puede demostrar para los sistemas continuos
$$ \large \begin{equation} x(t) = e^{st} \ y(t) = \int_{- \infty}^{+ \infty} h(\tau) x(t-\tau)\mathrm{d} \tau \ y(t) = \int_{- \infty}^{+ \infty} h(\tau) e^{s(t-\tau)}\mathrm{d} \tau \ y(t) = e^{st} {\underbrace{ \int_{- \infty}^{+ \infty} h(\tau) e^{-s \tau}\mathrm{d} \tau}_{H(s) \rightarrow \text{Constante Compleja}}} \ y(t) = H(s)e^{st} \end{equation} $$
Para los sistemas discretos
$$ \large \begin{equation} x[n] = Z^n \ y[n] = \sum_{k = - \infty}^{+ \infty} h[k]x[n-k] \ y[n] = \sum_{k = - \infty}^{+ \infty} h[k] Z^{n-k} \ y[n] = Z^n {\underbrace{ \sum_{k = - \infty}^{+ \infty} h[k] Z^-k}_{H[Z]}} \ y[n] = h[z]Z^n \end{equation} $$
En Resumen para los sistemas continuos $$ \large \begin{equation} x(t) = a_1 e^{s_1 t} + a_2 e^{s_2 t} + a_3 e^{s_3 t} \rightarrow \ a_1 e^{s_1 t} \rightarrow a_1 H(s_1) e^{s_1 t} \ a_2 e^{s_2 t} \rightarrow a_2 H(s_2) e^{s_2 t} \ a_3 e^{s_3 t} \rightarrow a_3 H(s_3) e^{s_3 t} \ y(t) = a_1 H(s_1) e^{s_1 t} + a_2 H(s_2) e^{s_2 t} + a_3 H(s_3) e^{s_3 t} \ \quad \ x(t) = \sum_{k} a_k e^{s_k t} \rightarrow y(t) = \sum_{k}a_k H(s_k) e^{s_k t} \end{equation} $$
Para los sistemas Discretos $$ \large \begin{equation} x[n] = \sum_{k} a_k Z_{k}^{n} \ y[n] = \sum_{k} a_k H(Z_k) Z_{k}^{n} \end{equation} $$
Representacion en Series de Fourier de señales Periodicas Continuas
$$ \large x(t) = x(t+T) \quad \forall : t \ \large \omega_0 = \frac{2 \pi}{T} \quad \text{Frecuencia Fundamental} \ \large x(t) = cos(\omega_0 t + \phi) \quad o \quad x(t) = e^{j(\omega_0 t + \phi)} $$
las señales exponenciales complejas que están relacionadas armónicamente cumplen que
$$ \large \phi_k(t) = e^{j k \omega_0 t} = e^{j k \left( \frac{2 \pi}{T}\right) t} \quad k = 0, \pm 1, \pm 2, … $$ SERIE DE FOURIER $$ \Large \boxed{x(t) = \sum_{k = - \infty}^{+ \infty}a_k e^{j k \omega_0 t} = \sum_{k = - \infty}^{+ \infty}a_k e^{j k \left( \frac{2 \pi}{T} \right) t} } $$
Ejemplo: $$ \large \begin{equation} x(t) = \sum_{k = -3}^{3}a_k e^{j k 2 \pi t}\ a_0 = 1, \quad a_1=a_{-1} = \frac{1}{4} \ a_2=a_{-2} = \frac{1}{2}, \qquad a_3=a_{-3} = \frac{1}{3} \ x(t) = 1 + \frac{1}{4} \left ( e^{j 2 \pi t} +e^{- j 2 \pi t} \right ) + \frac{1}{2} \left ( e^{j 4 \pi t} +e^{- j 4 \pi t} \right ) + \frac{1}{3} \left ( e^{j 6 \pi t} +e^{- j 6 \pi t} \right ) \rightarrow \ x(t) = 1 + \frac{1}{2}\cos(2 \pi t) + \cos(4 \pi t) + \frac{2}{3}\cos(6 \pi t) \end{equation} $$
Serie de Fourier para Señales Reales
$$ \large \text{Si} \quad \large x(t) \in \mathbb{Re} \rightarrow x^(t) = x(t) \ \large \rightarrow a_{-k}^ = a_k \rightarrow a_{k}^* = a_{-k} $$
Formas Alternativas para representar Series de Fourier
$$ \large x(t) = a_0 + \sum_{k=1}^{\infty}[a_k e^{j k \omega_0 t}+ a_{-k} e^{-j k \omega_0 t}] \rightarrow a_{-k}^* = a_k \ \large x(t) = a_0 + \sum_{k=1}^{\infty}[a_k e^{j k \omega_0 t}+ a_{k}^* e^{-j k \omega_0 t}] $$ Como son Complejos conjugados entonces $$ \large x(t) = a_0 + \sum_{k=1}^{\infty} 2 \mathbb{Re} \left { a_k e^{j k \omega_0 t} \right } $$ Si $a_k$ se expresa de forma polar entonces
$$ \large a_k = A_k e^{j \theta_k} \rightarrow \ \large x(t) = a_0 + \sum_{k=1}^{\infty} 2 \mathbb{Re} \left { A_k e^{j( k \omega_0 t + \theta_k)} \right } \ \large x(t) = a_0 + 2 \sum_{k=1}^{\infty} A_k \cos ( k \omega_0 t + \theta_k) $$ Que es llamada la serie de fourier de una señal periodica real continua, otra forma de representacion se obtiene cuando
$$ \large a_k = B_k +jC_k \rightarrow \ \large x(t) = a_0 + 2 \sum_{k=1}^{\infty}[ B_k \cos ( k \omega_0 t)- C_k \sin ( k \omega_0 t)] $$
Determinacion de la Serie de Fourier para una Señal Periodica Continua
Se demostrara como calcular los valores de $\large a_k$ $$ \large x(t)\qquad \quad = \sum_{k = - \infty}^{+ \infty}a_k e^{j k \omega_0 t} \ x(t) e^{-j n \omega_0 t} = \sum_{k = - \infty}^{+ \infty}a_k e^{j k \omega_0 t} : e^{-j n \omega_0 t} \ \int_0^T x(t) e^{-j n \omega_0 t} \mathbb{d}t= \int_0^T \sum_{k = - \infty}^{+ \infty}a_k e^{j k \omega_0 t} : e^{-j n \omega_0 t} \mathbb{d}t\ \int_0^T x(t) e^{-j n \omega_0 t} \mathbb{d}t= \sum_{k = - \infty}^{+ \infty}a_k {\underbrace{ \left [ \int_0^T e^{j (k -n)\omega_0 t} \mathbb{d}t \right ]}_{\large \bigstar}} \ \large \bigstar : \int_0^T e^{j (k -n)\omega_0 t} \mathbb{d}t = \int_0^T \cos((k-n)w_0 t) \mathbb{d}t + j\int_0^T \sin((k-n)w_0 t) \mathbb{d}t $$ En $\large \bigstar$ Si $\large k \neq n :$ entonces la integral es igual a cero
En $\large \bigstar$ Si $\large k = n :$ entonces $\large \int_0^T e^{j (k -n)\omega_0 t} \mathbb{d}t = T$
Finalmente reemplazando los valores obtenidos en $\bigstar$ ,cuando $k=n$, en la formula original podemos despejar y obtenemos:
$$ \large \boxed{a_k = \frac{1}{T}\int_0^T x(t)e^{-j k \omega_0 t} \mathbb{d}t} $$ $$ \large \boxed{a_0 = \frac{1}{T}\int_0^T x(t) \mathbb{d}t} $$ y recordando que la serie de Fourier es igual a:
$$ \Large \boxed{x(t) = \sum_{k = - \infty}^{+ \infty}a_k e^{j k \omega_0 t} = \sum_{k = - \infty}^{+ \infty}a_k e^{j k \left( \frac{2 \pi}{T} \right) t} } $$
Ejemplos de Calculo de la serie de Fourier
Determinar la serie de Fourier para $\large x(t) = \sin (\omega_0 t)$
Determinar la serie de Fourier para $\large x(t) = 1 + \sin (\omega_0 t) + 2 \cos (\omega_0 t) + \cos (2\omega_0 t + \frac{\pi}{4})$
Calculo Serie de Fourier de una señal cuadrada
Convergencia de las Series de Fourier
Para que se pueda calcular las series de Fourier se deben cumplir las condiciones de Dirichlet
Condicion 1
Sobre cualquier Periodo $x(t)$ debe ser absolutamente integrable. $$\large \int_T |x(t)| \mathbb{d}t < \infty $$
Condicion 2
La variacion de $x(t)$ en cualquier intervalo finito de tiempo debera estas acotado, entonces existe un numero finito de maximos y minimos durante un periodo.
Condicion 3
En cualquier intervalo finito de tiempo hay solo un numero finito de discontinuidades, ademas esas discontinuidades deben ser finitas.
Fenomeno de Gibss
El fenómeno de Gibbs es la descripción del comportamiento que tiene la serie de Fourier asociada a una función definida a trozos periódica en una discontinuidad no evitable de salto finito. Su nombre se debe a J. Willard Gibbs, quien fue el primero en explicar este fenómeno, en 1899.
Cuando la función que se está desarrollando en Serie de Fourier tiene discontinuidades (señales de variación rápida) no es posible que haya una buena convergencia en los entornos de las mismas.
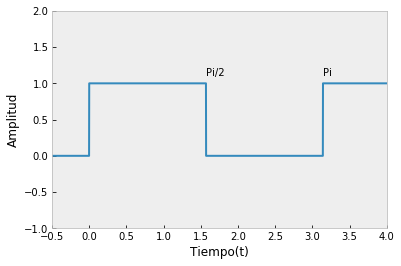
Señal Cuadrada
Esta señal es un buen ejemplo para demostrar el fenomeno de Gibbs
# Importar librerias basicas
import numpy as np
import matplotlib.pyplot as plt
import sympy as sym
%matplotlib inline
plt.style.use('bmh') # estilo de las graficas
from IPython.display import Latex # para visualizar ecuaciones en jupyter
from scipy import signal as sp
amplitud = 1
periodo = np.pi
t = np.arange(-1, 10, 0.001)
función = ((sp.square(2 * t)) * (amplitud / 2.0)) + (amplitud / 2.0)
plt.plot(t, función, lw=2)
plt.grid()
plt.annotate('Pi', xy = (np.pi, 1), xytext = (np.pi, 1.1))
plt.annotate('Pi/2', xy = (np.pi / 2.0, 1), xytext = (np.pi / 2.0, 1.1))
plt.ylabel('Amplitud')
plt.xlabel('Tiempo(t)')
plt.ylim(-1,2)
plt.xlim(-0.5, 4)
plt.show()
#Importamos todo el modulo sympy
%matplotlib inline
import numpy as np
import matplotlib.pylab as plt
from sympy import *
#ademas importamos las variables simbolicas 'n' y 't'
from sympy.abc import t, n
ao = integrate(2 / pi, (t, 0, pi / 2))
#integramos la función (2/pi) cuya variable es 't'
#y limites de integracion entre 0 y pi/2
print('Coeficientes de la serie de Fourier en forma Trigonometrica')
print("\n"+"a0 = ")
pprint(ao)
#Usamos la función pprint para mostrar ao
an = integrate((2 / pi) * cos(2 * n * t), (t, 0, pi / 2))
an = integrate((2 / pi) * cos(2 * n * t), (t, 0, pi / 2))
#integramos la función (2/pi)*cos(2nt)
#Su variable es 't' y sus limites de integracion son 0 y pi/2
print ("\n"+"an = ")
pprint(an)
#Usamos la función pprint para mostrar an
bn = together(integrate((2 / pi) * sin(2 * n * t), (t, 0, pi / 2)))
#integramos la función (2/pi*cos(2nt)
#Su variable es 't' y sus limites de integracion
#son 0 y pi/2. Ademas usamos la función "together"
#para simplificar la expresion
print("\n"+"bn = ")
pprint(bn)
#Usamos la función pprint para mostrar bn
print("\n"+"f(x) = ")
Coeficientes de la serie de Fourier en forma Trigonometrica
a0 =
1
an =
⎧sin(π⋅n)
⎪──────── for n > -∞ ∧ n < ∞ ∧ n ≠ 0
⎨ π⋅n
⎪
⎩ 1 otherwise
bn =
⎧ cos(π⋅n) 1
⎪- ──────── + ─── for n > -∞ ∧ n < ∞ ∧ n ≠ 0
⎨ π⋅n π⋅n
⎪
⎩ 0 otherwise
f(x) =
armonicos = 10
serie = (ao/2)
for i in range(1, armonicos + 1):
serie = serie + (an*cos(2*n*t)).subs(n, i)
for j in range(1, armonicos + 1):
serie = serie + (bn*sin(2*n*t)).subs(n, j)
pprint(serie)
#Usando el modulo para graficas de sympy
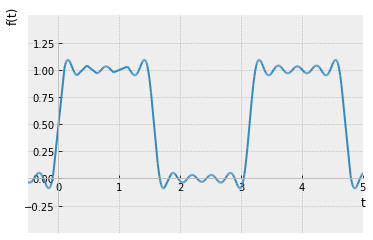
plotting.plot(serie, ylim=(-0.5, 1.5), xlim=(-0.5,5));
2⋅sin(2⋅t) 2⋅sin(6⋅t) 2⋅sin(10⋅t) 2⋅sin(14⋅t) 2⋅sin(18⋅t) 1
────────── + ────────── + ─────────── + ─────────── + ─────────── + ─
π 3⋅π 5⋅π 7⋅π 9⋅π 2
points = [1,2,4,10,30,50]
for ii in points:
armonicos = ii
serie = (ao/2)
for i in range(1, armonicos + 1):
serie = serie + (an*cos(2*n*t)).subs(n, i)
for j in range(1, armonicos + 1):
serie = serie + (bn*sin(2*n*t)).subs(n, j)
#Usando el modulo para graficas de sympy
print(f'Numero de terminos = {ii}')
sym.plotting.plot(serie, ylim=(-0.5, 1.5), xlim=(-0.5,5))
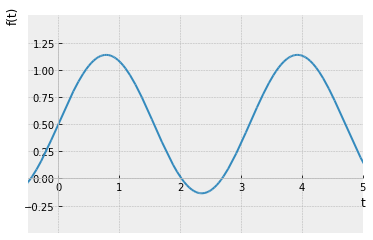
Numero de terminos = 1
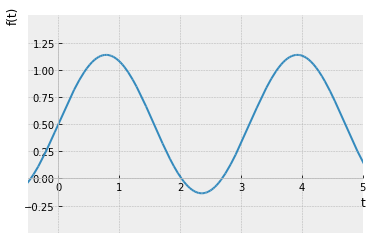
Numero de terminos = 2
Numero de terminos = 4
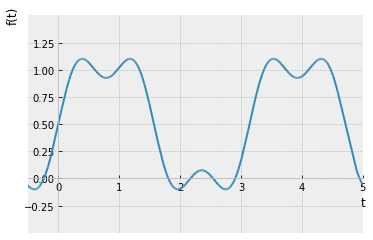
Numero de terminos = 10
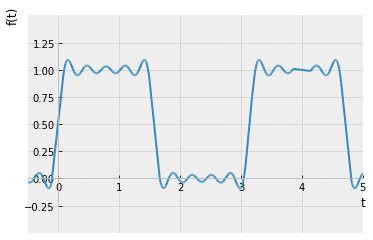
Numero de terminos = 30
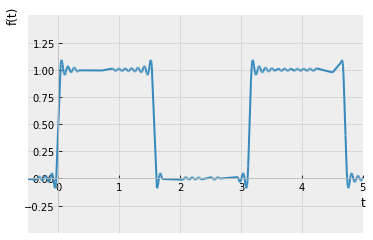
Numero de terminos = 50
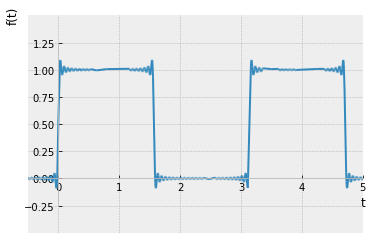
Como se puede apreciar, a medida que se suman más términos a la serie, ésta se va aproximando a la onda cuadrada dado que las oscilaciones se vuelven más rápidas y más pequeñas, pero los picos no disminuyen. Estos picos en las series de Fourier de la función cuadrada nunca desaparecen; son llamados el fenómeno de Gibbs nombrado por el físico estadounidense Josiah Willard Gibbs. Ocurren cada vez que las señales tienen discontinuidades de salto (generalmente en los extremos), y siempre estarán presentes cuando la señal tiene oscilaciones fuertes como en este caso de uno a menos uno.
Propiedades de la serie de Fourier
$$ \large x(t) \overset{fs}{\longleftrightarrow} a_k $$
Linealidad
$$ \large x(t) \overset{fs}{\longleftrightarrow} a_k \ \large y(t) \overset{fs}{\longleftrightarrow} b_k \ \large Z(t) = Ax(t) + By(t) \overset{fs}{\longleftrightarrow} C_k = Aa_k + Bb_k $$
Desplazamiento en el tiempo
$$ \large y(t) = x(t-t_0) \ \large b_k = \frac{1}{T} \int_T x(t-t_0)e^{-jk\omega_0t}\mathbb{d}t \ \text{Si hacemos} \quad \tau = t-t_0 \ \large b_k = \frac{1}{T} \int_T x(\tau)e^{-jk\omega_0 (\tau -t_0)}\mathbb{d}\tau \rightarrow \ \large b_k = \frac{e^{-j\omega_0t_0}}{T} \int_T x(\tau)e^{-jk\omega_0 (\tau)}\mathbb{d}\tau \rightarrow \ b_k = e^{-j\omega_0t_0} a_k \ \large \boxed{x(t-t_o)\overset{fs}{\longleftrightarrow}e^{-j\omega_0t_0} a_k} $$ Cuando una señal periodica se desplaza en $\large t$ las magnitudes de $\large |a_k| = |b_k|$ no se alteran
Inversion de tiempo
$$ y(t) = x(-t) \rightarrow x(-t) = \sum_{k = -\infty}^{\infty}a_k e^{-j k \omega_0 t} $$ Haciendo $k = -m \rightarrow$ $$ y(t) = x(-t) \rightarrow x(-t) = \sum_{m = -\infty}^{\infty}a_m e^{j m \omega_0 t} \rightarrow \large bk = a_{-k} \ \large \boxed{x(-t) \overset{fs}{\longleftrightarrow} a_{-k}} $$
- Si $\large x(t)$ es par $\large x(t) = x(-t)$ los coeficientes de fourier también lo son $\large a_k = a_{-k}$
- Si $\large x(t)$ es impar $\large -x(t) = x(-t)$ los coeficientes de fourier también lo son $\large -a_k = a_{-k}$
Escalamiento en el tiempo
El escalamiento hace que cambie el periodo de la señal
$$ \Large \boxed{x(\alpha t) = \sum_{k = - \infty}^{+ \infty}a_k e^{j k (\alpha\omega_0) t} } $$
Multiplicacion
$$ \large x(t) \overset{fs}{\longleftrightarrow} a_k \ \large y(t) \overset{fs}{\longleftrightarrow} b_k \ \large x(t)y(t) \overset{fs}{\longleftrightarrow} h_k = \sum_{L = -\infty}^{\infty}a_L b_{k-L} $$
Conjugacion
$$ \large x(t) \overset{fs}{\longleftrightarrow} a_k \ \large x(t)^* \overset{fs}{\longleftrightarrow} a^*_{-k} \ $$
Relacion de Parseval
$$ \large \frac{1}{T}\int_T |x(t)|^2 \mathbb{d}t= \sum_{k=-\infty }^{+ \infty}|a_k|^2 $$
Convolucion Periodica
$$ \large x(t)*y(t) = \int_T x(\tau)y(t-\tau)\mathbb{d}\tau \overset{fs}{\longleftrightarrow} T a_k b_k $$
Derivacion
$$ \large \frac{\mathbb{d}x(t)}{\mathbb{d}t} \overset{fs}{\longleftrightarrow} jk \omega_0 a_k = jk (\frac{2\pi}{T})a_k $$
Integracion
$$ \large \int_{- \infty}^{t}x(t)\mathbb{d}t \overset{fs}{\longleftrightarrow} \left ( \frac{1}{j k \omega_0} \right) a_k $$
Representacion en Series de Fourier de señales Periodicas Discretas
La principal diferencia con la serie continua, es que la serie discreta es finita, lo que indica que una señal discreta periodica se puede representar como una combinacion lineal de exponenciales complejas armonicas discretas
$$ \large x[n] = x[n+N] \qquad \omega_0 = \frac{2 \pi}{N} \quad \text{Frecuencia Fundamental} $$
las señales exponenciales complejas que estan relacionadas armónicamente cumplen que
$$ \large \phi_k[n] = e^{j k \omega_0 n} = e^{j k \left( \frac{2 \pi}{N}\right) t} \quad k = 0, \pm 1, \pm 2, … $$ Pero solo existen $N$ Señales distintas, debido a la periodicidad de las señales exponenciales complejas discretas, la serie discreta de fourier esta definida como:
$$ \Large
\boxed{x[n] = \sum_{k =
Determinacion de la Serie de Fourier para una Señal Periodica Discreta
Se demostrara como calcular los valores de $a_k$
$$
\large x[n]\qquad \quad = \sum_{k =
Resolviendo de la misma manera que para las serries continuas obtenemos que:
$$
\boxed{\large
\begin{aligned}
a_k &= \frac{1}{N} \sum_{n=
Ejemplos de Calculo de la serie de Fourier Discreta
Determinar la serie de Fourier para $\large x[n] = \sin (\omega_0 n)$
Calculo Serie de Fourier de una señal cuadrada
Fenomeno de Gibss
Para las señales discretas no se presenta el fenomeno de Gibbs, estas se representan completamente con componentes finitas, como se puede ver en la solucion de la señal cuadrada
Propiedades de la serie de Fourier Discreta
Las Propiedades son iguales a las de las señales continuas, a diferencia de estos casos:
Multiplicacion
$$
\large x[n] \overset{fs}{\longleftrightarrow} a_k \
\large y[n] \overset{fs}{\longleftrightarrow} b_k \
\large x[n]y[n] \overset{fs}{\longleftrightarrow} d_k = \sum_{L =
Primera Diferencia
$$ \large x[n] - x[n-1] \overset{fs}{\longleftrightarrow} (1- e^{-j k \frac{2 \pi}{N}})a_k $$
Relacion de Parseval
$$
\large \frac{1}{N} \sum_{n=
Serie de Fourier y Sistemas LTI
Para las señales continuas $$ \large x(t) = e^{st} \ y(t) = H(s)e^{st} \ H(s) = \int_{- \infty}^{+ \infty} h(\tau) e^{-s \tau}\mathrm{d} \tau $$ En la cual $\large h(t)$ es la respuesta al impulso
Para las señales discretas
Si $\large s ,z$ con señales complejas generales $\large H(s), H[Z]$ se conocen como las funciones del sistema.
Si $\large s=j \omega$ entonces $\large H(j\omega)$ es la Respuesta en frecuencia
$$ \large \boxed{ H(j\omega) = \int_{- \infty}^{+ \infty} h(\tau) e^{-s \tau}\mathrm{d} \tau} $$
Entonces si:
$$ \large x(t) = \sum_{k = - \infty}^{+ \infty}a_k e^{j k (\omega_0) t} \rightarrow \ y(t) = \sum_{k = - \infty}^{+ \infty}a_k H(e^{j\omega_0}) e^{j k (\omega_0) t} $$ Donde $\large y(t)$ también es periodica con la misma frecuencia fundamental de $\large x(t)$
Para las Señales discretas $\large |Z| =1$ donde $\large Z = e^{j\omega}$ $$ \large \boxed{ H(e^{j\omega}) = \sum_{n = -\infty}^{+ \infty} h[n] e^{-j \omega n}} $$
$$
\large x[n] = \sum_{k =
REFERENCIAS
- Capitulo 3 Oppenheim, Sistemas y Señales
- http://raerpo2.blogspot.com/2011/01/series-de-fourier-con-python.html
- https://nbviewer.jupyter.org/github/spatialaudio/signals-and-systems-lecture/blob/master/periodic_signals/fourier_series.ipynb
- https://staff.fnwi.uva.nl/r.vandenboomgaard/SP20162017/FrequencyDomain/CTP.html
Phd. Jose R. Zapata
