1.1 Transformacion de Variable Independiente

Modificacion basicas de la variable independiente, generalemente el tiempo. Permiten introducir varias propiedades basicas de los sistemas y señales

# importar librerias de python

import sympy as sym # Libreria de operaciones matematicass simbolicas
import matplotlib.pyplot as plt
plt.style.use('bmh') # estilo de las graficas
%matplotlib inline

from IPython.display import Latex # para visualizar ecuaciones en jupyter

#sym.init_printing()

definición de la función a graficar que se usara como ejemplo

#definición de t como variable simbolica
t = sym.symbols('t', real=True)

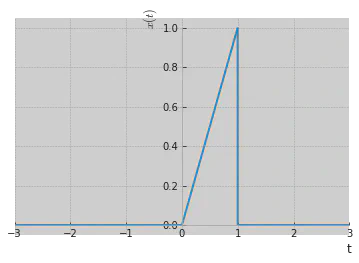
# función en forma de triangulo
trian = t*sym.Heaviside(t) - t*sym.Heaviside(t - 1)

# Grafica de la función creada
print('x(t) = ')
sym.plot(trian,(t, -3, 3),  ylabel=r'$x(t)$');

x(t) =

Corrimiento del tiempo ( Temporal Shift)

Una señal $x(t)$ o $x[n]$ que se retrasa por $\tau$ segundos se representa como una versión desplazada hacia la derecha el eje t.

Una señal desplazada en el tiempo $x(t)$ es definida como

\begin{equation} y(t) = x(t-\tau) \end{equation} con $\tau \in \mathbb{R}$. La señal $x(t)$ es

Desplazada a La derecha (retrazada) para $\tau>0$
- Señal continua $x(t−\tau)$
- Señal discreta $x[n − \tau]$

Ejemplo: Sonares, señales de sismos, radares, señales de varios sensores en diferentes posiciones

# Correr la función 1 segundo
print('x(t) = ')
sym.plot(trian,(t, -3, 3),  ylabel=r'$x(t)$');

print('x(t-1) = ')
x = trian.subs(t, t-1)
sym.plot(x,(t, -3, 3),  ylabel=r'$x(t-1)$', line_color='red');

x(t) =

x(t-1) =

Desplazada a La izquierda (adelantada) si $\tau < 0$
- Señal continua $x(t + \tau)$
- Señal discreta $x[n + \tau]$

# Correr la función 1 segundo
x = trian.subs(t, t+2)
print('x(t) = ')
sym.plot(trian,(t, -3, 3),  ylabel=r'$x(t)$');
print('x(t+1) = ')
sym.plot(x,(t, -3, 3),  ylabel=r'$x(t+2)$', line_color='red');

x(t) =

x(t+1) =

Inversion en el Tiempo (Temporal Flipping)

La inversion en el tiempo de una señal $x(t)$ esta definida como \begin{equation} y(t) = x(- t) \end{equation} Se interpreta geometricamente como el reflejo de la señal respecto al eje vertical

# invertir la función en el tiempo

#Grafica Original
print('x(t) = ')
sym.plot(trian,(t, -3, 3),  ylabel=r'$x(t)$');

# Inversion
x = trian.subs(t, -t)
# Grafica de la función modificada
print('x(-t) = ')
sym.plot(x,(t, -3, 3),  ylabel=r'$x(-t)$', line_color='red');

x(t) =

x(-t) =

Escalamiento en el tiempo (Temporal Scaling)

La compresión o expansión de la señal en el tiempo es conocida como escalamiento en el tiempo.

El escalamiento temporal de la señal $x(t)$ se define como

\begin{equation} y(t) = x(a \cdot t) \end{equation}

con $a \in \mathbb{R}$. La señal $x(t)$ es

Estirada o expandida para $0 < a < 1$
Comprimida para $a > 1$
Invertida en el tiempo y escalda para $a < 0$

Una aplicacaion del escalamiento temporal en procesamiento de señales en la adaptacion de la escala de tiempo para el modelamiento del efecto Doppler.

# Escalamiento temporal por un numero menor que 1

#Grafica Original
print('x(t) = ')
sym.plot(trian,(t, -3, 3),  ylabel=r'$x(t)$');

# Escalamiento por 0.5
a = .5
x = trian.subs(t, a*t)
display(Latex(r'$\large x \left (\frac{1}{2} t \right)$'))
# Grafica de la función modificada
sym.plot(x,(t, -3, 3),  ylabel=r'$x(1/2*t)$', line_color='red');

x(t) =

$\large x \left (\frac{1}{2} t \right)$

# Escalamiento temporal por un numero mayor que 1

#Grafica Original
print('x(t) = ')
sym.plot(trian,(t, -3, 3),  ylabel=r'$x(t)$', title = 'x(t)');

# Escalamiento por 0.5
a = 2
x = trian.subs(t, a*t)
# Grafica de la función modificada

display(Latex(r'$\large x \left ( 2 t \right)$'))

sym.plot(x,(t, -3, 3),  ylabel=r'$x(2*t)$', line_color='red');

x(t) =

$\large x \left ( 2 t \right)$

Transformacion General

El efecto de transformar la variable independiente de una señal $x(t)$ para obtener la señal modificada es de la forma:

\begin{equation} y(t) = x(a \cdot t +b) \end{equation}

Con la transformación, la variable independiente conserva la forma de x(t). La señal puede ser:

Alargada linealmente cuando $|a| < 1$ ,
Comprimida si $|a| > 1$,
Invertida en el tiempo si $a < 0$, y
Desplazada en el tiempo si $b$ es diferente de cero.
- siendo desplazada a la derecha si se resta el valor de $|b|$
- siendo desplazada a la izquierda si se suma el valor de $|b|$

Nota: Primero se hace el desplazamiento y luego se escala

# Transformaciones Generales

#Grafica Original
print('x(t) = ')
sym.plot(trian,(t, -3, 3),  ylabel=r'$x(t)$');

# Escalamiento por 0.5
a = .5
# Desplazamiento de -1
x = trian.subs(t, a*t+1)
# Grafica de la función modificada
display(Latex(r'$\large x \left (\frac{1}{2} t +1\right)$'))
sym.plot(x,(t, -3, 3),  ylabel=r'$x(1/2*t+1)$', line_color='red');

x(t) =

$\large x \left (\frac{1}{2} t +1\right)$

# Transformaciones Generales

#Grafica Original
print('Otro Ejemplo = ')
print('x(t) = ')
sym.plot(trian,(t, -3, 3),  ylabel=r'$x(t)$');

# Escalamiento por -3
a = -3
# Desplazamiento de 2
x = trian.subs(t, a*t-2)
# Grafica de la función modificada
display(Latex(r'$\large x \left ( -3 t -2 \right)$'))
sym.plot(x,(t, -3, 3),  ylabel=r'$x(-3*t-2)$', line_color='red');

Otro Ejemplo =
x(t) =

$\large x \left ( -3 t -2 \right)$

Cambio de Amplitud de la señal

Estos cambios no se realizan en la variable independiente, si no que afectan la amplitud de la señal

#Grafica Original
print('x(t) = ')
sym.plot(trian,(t, -3, 3),  ylabel=r'$x(t)$')

# Multiplicar por dos la amplitud
print('2 x(t) = ')
sym.plot(2*trian,(t, -3, 3),  ylabel=r'$2*x(t)$');

x(t) =

2 x(t) =

#Grafica Original
print('x(t) = ')
sym.plot(trian,(t, -3, 3),  ylabel=r'$x(t)$')

# Multiplicar por dos la amplitud
print('-2 x(t) = ')
sym.plot(-2*trian,(t, -3, 3),  ylabel=r'$-2*x(t)$');

x(t) =

-2 x(t) =

REFERENCIAS

Phd. Jose R. Zapata