Discretas
Impulso Unitario (dirac)
\begin{equation} \large \delta[n] = \begin{cases} 1, & n = 0 \ 0, & n \neq 0 \end{cases} \end{equation}
import numpy as np
import matplotlib.pyplot as plt
import sympy as sym
%matplotlib inline
plt.style.use('bmh') # estilo de las graficas
from IPython.display import Latex # para visualizar ecuaciones en jupyter
def dirac(n):
return np.where(n == 0, 1.0, 0.0)
n = np.arange(-10, 11)
x = dirac(n)
plt.stem(n, x, use_line_collection=True)
plt.xlabel('$n$')
plt.title('Impulso Unitario')
plt.ylabel('$\delta[n]$')
plt.ylim([-0.1, 1.1]);

Escalon Unitario (Heaviside)
\begin{equation} \large \mu[n] = \begin{cases} 1, & n \geq 0 \ 0, & n < 0 \end{cases} \end{equation}
# definiendo la función heaviside en dominio discreto
def heaviside(n):
return np.where(n >= 0, 1.0, 0.0)
n = np.arange(-5, 20)
x = heaviside(n)
plt.stem(n, x, use_line_collection=True)
plt.xlabel('$n$')
plt.title('Escalon Unitario')
plt.ylabel('$\mu [n]$')
plt.ylim([-0.1, 1.1]);

Rampa
\begin{equation} \large r[n] = \begin{cases} n , & n \geq 0 \ 0 , & n < 0 \end{cases} \end{equation} El valor que multiplique la función rampa modificara la pendiente de la señal.
# definiendo la función rampa en dominio discreto
def rampa(n):
return n*(np.where(n >= 0, 1.0, 0.0))
n = np.arange(-5, 20)
x = rampa(n)
plt.stem(n, x, use_line_collection=True)
plt.xlabel('$n$')
plt.title('Rampa Discreta')
plt.ylabel('$r[n]$')
plt.ylim([-0.1, 20]);

Relaciones entre las funciones
\begin{equation} \large \delta[n] = \mu[n]-\mu[n-1] \end{equation} \begin{equation} \large \mu[n] = \sum_{m=0}^{\infty} \delta[m] = \sum_{k=0}^{\infty} \delta[n-k] \end{equation}
\begin{equation} \large r[n] = n \mu[n] \end{equation}
A partir de las ecuaciones anteriores se puede deducir que la función impulso es la primera derivada del escalón y el escalón es la primera derivada de la función rampa.
La secuencia impulso unitario (ecuación 5) se puede utilizar para obtener muestras del valor de una señal en $n=0 \rightarrow x[n]\delta[n] = x[0]\delta[n]$
De forma general, EL muestreo del impulso unitario esta definido como : $x[n]\delta[n-n_{0}] = x[n_{0}]\delta[n-n_{0}]$
Continuas
Impulso Unitario (dirac)
El impulso unitario $\delta (t)$ es una función definida primero por Paul Dirac de la forma: \begin{equation} \large \delta(t)= \begin{cases} 1, & t = 0 \ 0, & t \neq 0\end{cases} \end{equation} Se puede ver al impulso como un pulso rectangular con ancho infinitesimal y de área unitaria. \begin{equation} \large \int_{-\infty}^{\infty} \delta(t) dt = 1 \end{equation}
Matematica y teoricamente se representa como una flecha con altura de 1 de la siguiente manera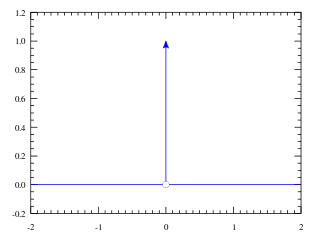
El impulso de Dirac es una de las señales más importantes en la teoría de sistemas y señales. Se utiliza para la caracterización de sistemas Lineales e invariantes en el tiempo (LTI) y el modelado de señales por medio de impulsos.
import numpy as np
rojo = '\033[91m' # para imprimir con color rojo
finrojo = '\033[0m'
msg = ('Nota importante: \n'
'Solo por ilustracion en Python se realiza la siguiente grafica,\n'
'ya que es un infinitesimal, entonces no se podria ver')
print(rojo+msg+finrojo)
# el código siguiente solo es para hacer una ilustracion
# de la señal impulso, sin ser de esta forma verdaderamente
# INGRESO
def u(t): return np.piecewise(t, t >= 0, [1, 0])
a = -10
b = 10
dt = 0.1
t = np.arange(a, b, dt)
u0 = u(t)
udt = u(t-dt)
impulso = u0 - udt
# SALIDA - GRAFICA
plt.figure(4)
plt.plot(t, impulso)
plt.margins(dt)
plt.xlabel('t')
plt.ylabel('$\delta (t)$')
plt.title('impulso()');
[91mNota importante:
Solo por ilustracion en Python se realiza la siguiente grafica,
ya que es un infinitesimal, entonces no se podria ver[0m

# importar librerias
import sympy as sym
t = sym.symbols('t', real=True)
print('definición de la función impulso')
delta = sym.DiracDelta(t)
delta
definición de la función impulso
$\displaystyle \delta\left(t\right)$
display(Latex('$\int_{-\infty}^{\infty} \delta(t) dt =$'))
sym.integrate(delta, (t, -sym.oo, sym.oo))
$\int_{-\infty}^{\infty} \delta(t) dt =$
$\displaystyle 1$
El impulso es el pulso mas corto que se puede aplicar a un sistema, la respuesta no sera influenciado por la duracion del pulso o por la forma del pulso; sino por el efecto neto integrado del pulso, es decir su area.
Al igual que con las señales discretas: $t=0 \rightarrow x(t)\delta(t) = x(0)\delta(t)$
De forma general, El muestreo del impulso unitario esta definido como : $x(n)\delta(t-t_{0}) = x(t_{0})\delta(t-t_{0})$
Escalon Unitario (Heaviside)
El escalon unitario continuo esta definido como: \begin{equation} \large \mu(t)= \begin{cases} 1, & t\geq 0 \ 0, & t<0\end{cases} \end{equation} Tiene una discontinuidad en $t=0$
En Python se define asi $\theta (t)$
print('definición de la función Escalon Unitario')
paso = sym.Heaviside(t)
paso
definición de la función Escalon Unitario
$\displaystyle \theta\left(t\right)$
sym.plot(paso, (t, -2, 2), ylim=[-0.2, 1.2],
ylabel='$\mu(t)$', title='Escalon Unitario');

Rampa
\begin{equation} \large r(t) = \begin{cases} t , & t \geq 0 \ 0 , & t < 0 \end{cases} \end{equation} El valor que multiplique la función rampa modificara la pendiente de la señal.
print('definición de la función Rampa')
rampa = t*sym.Heaviside(t)
rampa
definición de la función Rampa
$\displaystyle t \theta\left(t\right)$
sym.plot(rampa, (t, -2, 4), ylim=[-0.2, 4],
ylabel='$r(t)$', title='Rampa');

Relaciones entre las funciones
El escalon unitario continuo es la integral del impulso unitario \begin{equation} \large \mu (t) = \int_{-\infty}^{t} \delta(\tau) d\tau \end{equation}
\begin{equation} \large \delta (t) = \frac{\mathrm{d} \mu (t) }{\mathrm{d} t} \end{equation} Lo anterior no es formalmente diferenciable
\begin{equation} \large r(t) = t \mu (t) \end{equation}
REFERENCIAS
Oppenheim 1.4
Phd. Jose R. Zapata
