Son los Bloques fundamentales para construir otras señales tanto continuas como discretas
Señal Continua Exponencial Compleja y Sinusoidal
Es de la Forma general: \begin{equation} \large x(t) = Ce^{s t} :::::: C,s \in \mathbb{Co} \end{equation}
Tener en cuenta que a la señal copmleja tambein la multiplica un termino que es de carácter exponencial.
De forma general solo mirando señal compleja exponencial es de la forma: $\large e^{st}$ donde: $s = \sigma + j\omega$ y $s^* = \sigma - j\omega$
Recordando la formula de Euler \begin{equation} \large e^{j \omega t} = \cos(\omega t) + j\sin(\omega t) \ \large e^{-j \omega t} = \cos(\omega t) - j\sin(\omega t) \end{equation}
Descomponiendo este termino tenemos:
$$ \large \begin{align} e^{st} &= e^{(\sigma + j\omega)t} \ &= e^{\sigma t} e^{j\omega t} \ &= e^{\sigma t} (\cos (\omega t) + j \sin (\omega t)) \end{align} $$
Dependiendo de esos parametros la señal toma diferentes formas.
Señal Exponencial Real
\begin{equation} \large x(t) = Ce^{s t} :::::: C,s \in \mathbb{Re} \ \large \sigma \neq 0 : y : \omega = 0 \end{equation}
from IPython.display import Latex # para visualizar ecuaciones en jupyter
import sympy as sym
import matplotlib.pyplot as plt
#plt.style.use('fivethirtyeight') # estilo de las graficas
plt.style.use('bmh') # estilo de las graficas
%matplotlib inline
#sym.init_printing()
t, sigma, omega = sym.symbols('t sigma omega', real=True)
s = sigma + 1j*omega
c = 2
x = c*sym.exp(s*t)
display(Latex('$\large x(t) = 2e^{2 t}, \quad C=2, s=(2+j0)$'))
sym.plot(x.subs({sigma: 2, omega: 0}), (t, -2, 2),
ylim=[-0.5, 30], ylabel='$x(t)$', legend=True);
$\large x(t) = 2e^{2 t}, \quad C=2, s=(2+j0)$

t, sigma, omega = sym.symbols('t sigma omega', real=True)
s = sigma + 1j*omega
c = 5
x = c*sym.exp(s*t)
display(Latex('$\large x(t) = 5e^{-2 t}, \quad C=5, s=(-2+j0)$'))
sym.plot(x.subs({sigma: -2, omega: 0}), (t, -2, 2),
ylim=[-0.2, 30], ylabel='$x(t)$', legend=True);
$\large x(t) = 5e^{-2 t}, \quad C=5, s=(-2+j0)$

Si $a=0$ entonces $x(t) = Kte$
t, sigma, omega = sym.symbols('t sigma omega', real=True)
s = sigma + 1j*omega
c = 2
x = c*sym.exp(s*t)
display(Latex('$\large x(t) = 2e^{0 t} \quad C=2, s=(0+j0)$'))
sym.plot(x.subs({sigma: 0, omega: 0}), (t, -2, 2),
ylim=[-0.2, 2.5], ylabel='$x(t)$', legend=True);
$\large x(t) = 2e^{0 t} \quad C=2, s=(0+j0)$

En resumen si $\sigma \neq 0 : y : \omega = 0$ entonces tenemos:
- Exponencial decreciente en el tiempo para $\sigma < 0$,
- Valor constante en el tiempo para $\sigma = 0$
- Exponencial creciente en el tiempo para $\sigma > 0$
Señal Sinusoidal o Periodica Exponencial Compleja
\begin{equation} \large x(t) = e^{j \omega_{0} t} \end{equation}
Como $\large x(t) = e^{j \omega_{0} t}$ es periodica entonces: \begin{equation} \large e^{j \omega_{0} t} = e^{j \omega_{0} (t+T)} \rightarrow e^{j \omega_{0} t} = e^{j \omega_{0} t} e^{j \omega_{0} T} \end{equation} Para que lo anterior se cumpla entonces: \begin{equation} \large e^{j \omega_{0} T} = 1 \ \large \text{Si} : \omega_{0}=0 \rightarrow x(t)=1 : \text{es periodica} : \forall : T \ \large \text{Si} : \omega_{0} \neq 0 \rightarrow \text{El Periodo fundamental $T_{0}$ de $x(t)$ es } T_{0}=\frac{2\pi}{|\omega_{0}|} \end{equation}
$T_{0}$ es inversamente proporcional a $|\omega_{0}|$ y Las señales $\large e^{j \omega_{0} t}$ y $\large e^{-j \omega_{0} t}$ tienen el mismo periodo fundamental.
Una señal que esta muy relacionada con la señal periodica compleja es la senusoidal: $x(t) = A \cos(\omega t + \phi)$ recordar que $\omega=2\pi f$ y $T=\frac{2\pi}{\omega}$
las unidades son $t[=]seg ,: \omega[=]\frac{rad}{seg} ,: \phi[=]rad$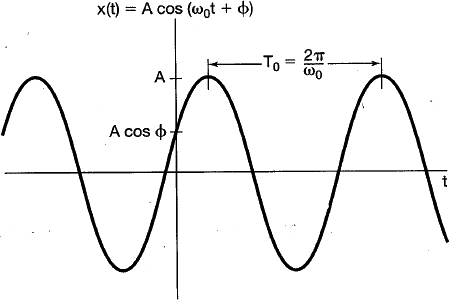
Apartir de la ecuación de Euler se puede obtener que: $$ \large \begin{align} A\cos(\omega_{0}t+\phi) &= \frac{A}{2}e^{j\phi}e^{j\omega_{0} t}+\frac{A}{2}e^{-j\phi}e^{-j\omega_{0} t} \ A\cos(\omega_{0}t+\phi) &= A \cdot \mathbb{Re}{e^{j(\omega_{0}t+\phi}} \ A\sin(\omega_{0}t+\phi) &= A \cdot \mathbb{Im}{e^{j(\omega_{0}t+\phi}} \end{align} $$
t, sigma, omega = sym.symbols('t sigma omega', real=True)
s = sigma + 1j*omega
c = 2
x = c * sym.exp(s*t)
# sustitucion de los valores
y = x.subs({omega: 5, sigma: 0})
display(Latex(
'$\large s = \sigma + j\omega_{0} \quad para \quad \sigma=0 , \omega_{0} =5$'))
display(Latex('$\large x(t) = 2\cos(5t)$'))
sym.plot(sym.re(y), (t, 0, 2*sym.pi), ylabel='x(t)', title='Re{$e^{st}$}')
display(Latex('$\large x(t) = 2\sin(5t)$'))
sym.plot(sym.im(y), (t, 0, 2*sym.pi), ylabel='x(t)',
title='Im{$e^{st}$}', line_color='r');
$\large s = \sigma + j\omega_{0} \quad para \quad \sigma=0 , \omega_{0} =5$
$\large x(t) = 2\cos(5t)$

$\large x(t) = 2\sin(5t)$

Las señales periodicas y en particular la señal periodica $\large e^{j \omega t }$ son ejemplo de señales con:
| $\large E_{\infty}=\infty$ | $\large P_{\infty}=1$ |
|---|---|
| $\large E_{periodo} = T_{0}$ | $\large P_{periodo} = \frac{1}{T_{0}}E_{periodo}=1$ |
Frecuencia Fundamental y Armonicos
Si $\large e^{j\omega T_{0}}=1$ entonces $\omega T_{0}$ tiene que ser multiplo de $2\pi$
$\omega T_{0} = 2\pi k$ para $k=0, \pm1, \pm2, \pm3, … \forall k \in \mathbb{Z} $
Si se define \begin{equation} \large\omega_{0}=\frac{2\pi}{T_{0}} \end{equation}
entonces $\omega$ tiene que ser un multiplo de $\omega_{0}$. se obtiene una familia de señales $\phi_{k}(t)$ que cumplen \begin{equation} \large \phi_{k}(t)=e^{j k \omega_{0}} ::::: \text{para} ::::K=0, \pm1, \pm2, \pm3, … \end{equation} Si $k=0 \rightarrow \phi_{k}(t) = constante$
Si $k \neq 0 \rightarrow \phi_{k}(t)$ es armonica con frecuencia fundamental $f_{0}=|k|\omega_{0} ::$ reemplazando en la ecuación (13). \begin{equation} \large \frac{2\pi}{|k|\omega_{0}} = \frac{T_{0}}{|k|} \end{equation}
- Esta Familia de señales esta conformada por la que tiene la frecuencia fundamental $k = \pm1$ y los armonicos $\forall :: k \in \mathbb{Z} \neq 1$
t, omega = sym.symbols('t omega', real=True)
x1 = sym.sin(omega*t)
# sustitucion de los valores
y1 = x1.subs({omega: 2})
y2 = x1.subs({omega: 4})
y3 = x1.subs({omega: 8})
p1 = sym.plot(y1, (t, 0, 2*sym.pi),
ylabel='$\phi_{k}(t)$', title='Familia de señales $\phi_{k}(t)$',
line_color='navy', legend=True, show=False)
p2 = sym.plot(y2, (t, 0, 2*sym.pi), line_color='r',
legend=True, show=False)
p3 = sym.plot(y3, (t, 0, 2*sym.pi), line_color='green',
legend=True, show=False)
p1.extend(p2)
p1.extend(p3)
p1.show()

Señal Exponencial Compleja General
Si $x(t) = Ce^{s t} :::: C,s \in \mathbb{Co}$, podemos escribir $C$ en forma polar y tendriamos. \begin{equation} \large C = |C|e^{j\theta} :::: s = \sigma+j\omega, \end{equation}
tenemos: \begin{equation} \large x(t) = Ce^{s t} = |C|e^{j\theta}e^{(\sigma+j\omega)t} = |C|e^{\sigma t}e^{j(\omega t+\theta)} \ \large x(t) = Ce^{s t} = |C|e^{\sigma t}\cos(\omega t+\theta) + j|C|e^{\sigma t}\sin(\omega t+\theta) \end{equation}
Donde podemos ver que tiene la forma de una función exponencial compleja (periódica) multiplicada por una exponencial.
- Si $\sigma = 0 \rightarrow$ señal sinusoidal
- Si $\sigma > 0 \rightarrow$ señal sinusoidal exponencialmente creciente
- Si $\sigma < 0 \rightarrow$ señal sinusoidal exponencialmente decreciente
La envolvente sera igual a $\large \pm|C|e^{\sigma t}$
t, sigma, omega = sym.symbols('t sigma omega', real=True)
s = sigma + 1j*omega
c = 3
x = c*sym.exp(s*t)
# Valores de sigma y omega
y = x.subs({sigma: -0.8, omega: 10 })
display(Latex('$\large x(t) = Ce^{s t} \quad C = 3, s = (-0.8 + j10)$'))
sym.plot(sym.re(y), (t, 0, 2*sym.pi), ylabel='x(t)', title = 'Re{$e^{st}$}');
$\large x(t) = Ce^{s t} \quad C = 3, s = (-0.8 + j10)$

t, sigma, omega = sym.symbols('t sigma omega', real=True)
s = sigma + 1j*omega
c = 2
x = c*sym.exp(s*t)
# Valores de sigma y omega
y = x.subs({sigma: 0.7, omega: 8 })
display(Latex('$\large x(t) = Ce^{s t} \quad C = 2, s = (0.7 + j8)$'))
sym.plot(sym.re(y), (t, 0, 2*sym.pi), ylabel='Re{$e^{st}$}');
$\large x(t) = Ce^{s t} \quad C = 2, s = (0.7 + j8)$

Ejemplo
t, sigma, omega = sym.symbols('t sigma omega', real=True)
s = sigma + 1j*omega
c = 1.5
x = c*sym.exp(s*t)
# Valores de sigma y omega
valor_sigma = 0.5
valor_omega = 6
y = x.subs({sigma: valor_sigma, omega: valor_omega})
y_exp = x.subs({sigma: valor_sigma, omega: 0})
display(Latex('$\large x(t) = C e^{st}$'))
display(Latex(f'$\large C = {c}, s = ({valor_sigma} + j{valor_omega})$'))
p1 = sym.plot(sym.re(y), (t, 0, 2*sym.pi),
ylabel='Re{$e^{st}$}', legend=True, show=False)
p2 = sym.plot(sym.re(y_exp), (t, 0, 2*sym.pi),
line_color='r', legend=True, show=False)
p3 = sym.plot(sym.re(-y_exp), (t, 0, 2*sym.pi),
line_color='r', legend=True, show=False)
p1.extend(p2) # agregar la grafica p2
p1.extend(p3) # agregar la grafica p3
p1.show()
$\large x(t) = C e^{st}$
$\large C = 1.5, s = (0.5 + j6)$

Señales Discretas Exponencial Compleja y Senoidal
Para el caso de señales discretas, tenemos la secuencia o Señal Discreta Exponencial Compleja: \begin{equation} \large x[n] = Ca^n, ::: C, a \in \mathbb{Co} \end{equation} También podemos expresarla, haciendo: \begin{equation} \large a = e^\beta \rightarrow x[n] = Ce^{\beta n} \end{equation}
Señal Discreta Exponencial Rea. En este caso, si α<0, el signo de x[n] se alterna.
Señal Discreta Exponencial Real
$x[n] = Ca^n$ donde $C, a \in \mathbb{Re}$
Dependiendo del valor de $a$ se tienen diferentes comportamientos
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
# parametros de la señal
n = np.arange(10)
c = 1
beta = 1
x = c*np.exp(beta*n)
display(Latex('$\large |a| > 1$'))
# grafica normal
plt.stem(n, np.real(x), use_line_collection=True)
plt.xlabel('$n$')
plt.xticks(list(n))
# para agregar los valores de cada punto
#for a, b in zip(n,x):
# plt.text(a, b, str(int(b)))
plt.ylabel('$x[n]$');
$\large |a| > 1$

n = np.arange(10)
c = 1
beta = -1
x = c*np.exp(beta*n)
display(Latex('$\large |a| < 1$'))
plt.stem(n, np.real(x), use_line_collection=True) #grafica normal
plt.xlabel('$n$')
plt.xticks(list(n))
plt.ylabel('$x[n]$');
$\large |a| < 1$

n = np.arange(10)
c = 1
beta = 0
x = c*np.exp(beta*n)
display(Latex('$\large |a| = 1 = constante$'))
plt.stem(n, np.real(x), use_line_collection=True)
plt.xlabel('$n$')
plt.xticks(list(n))
plt.ylabel('$x[n]$');
$\large |a| = 1 = constante$

n = np.arange(10)
c = 1
x = c*(-0.5)**n
display(Latex('$\large -1 < a < 0 $'))
plt.stem(n, x, use_line_collection=True)
plt.xlabel('$n$')
plt.xticks(list(n))
plt.ylabel('$x[n]$');
$\large -1 < a < 0 $

n = np.arange(10)
c = 1
x = c*(-1.5)**n
display(Latex('$\large a<-1$'))
plt.stem(n, x, use_line_collection=True)
plt.xlabel('$n$')
plt.xticks(list(n))
plt.ylabel('$x[n]$');
$\large a<-1$

n = np.arange(10)
c = 1
x = c*(-1)**n
plt.figure(figsize=(10, 4))
display(Latex('$\large a=-1$, En este caso la señal varia entre $+C$ y $-C$'))
plt.stem(n, x, use_line_collection=True)
plt.xlabel('$n$')
plt.xticks(list(n))
plt.ylabel('$x[n]$');
$\large a=-1$, En este caso la señal varia entre $+C$ y $-C$

Señal Sinusoidal o Periodica Exponencial Compleja
Esta señal discreta se obtiene cuando $\beta \in \mathbb{Co} :y: |a|=1 $ entonces: \begin{equation} \large x[n] = e^{j (\omega_{0} n + \phi)} \ \large x[n] = A \cos(\omega_{0} n + \phi) \end{equation} Si tomamos a $n$ como adimensional $\large \rightarrow \omega_{0}, \phi [=]rad$
Estas señales tienen $\large E_{\infty}=\infty:,: \large P_{Periodo}=finita :,: |e^{j \omega n}| = 1$
n = np.arange(31)
Omega = 2*np.pi/12
exp_sin = np.exp(1j * Omega * n)
display(Latex(r'$\large x[n] = \cos \left( \frac{2 \pi}{12} n \right ) \quad Periodo = 12$'))
plt.figure(figsize=(14, 4))
plt.stem(n, np.real(exp_sin), use_line_collection=True)
plt.xlabel('$n$')
plt.xticks(list(n)) # para graficar todos los números del eje x
plt.ylabel('$\Re \{ x[n] \}$');
$\large x[n] = \cos \left( \frac{2 \pi}{12} n \right ) \quad Periodo = 12$

Señal Exponencial Compleja General
Si $x[n] = Ca^{n} :::: C,a \in \mathbb{Co}$, podemos escribir $C$ y $a$ en forma polar y tendriamos. \begin{equation} \large C = |C|e^{j\theta} :::: a =|a|e^{j\omega_{0}} , \end{equation}
tenemos: \begin{equation} \large x[n] = Ca^{n} = |C||a|^n \cos(\omega_{0} t+\theta) + j|C||a|^n\sin(\omega_{0} t+\theta) \end{equation}
Donde podemos ver que tiene la forma de una función exponencial compleja (periódica) multiplicada por una exponencial.
- Si $|a| = 1 \rightarrow$ señal sinusoidal
- Si $|a| > 1 \rightarrow$ señal sinusoidal exponencialmente creciente
- Si $|a| <1 \rightarrow$ señal sinusoidal exponencialmente decreciente
n = np.arange(31)
Omega = 2*np.pi/12
exp_dec_sin = (np.abs(0.9)**n)*np.exp(1j * Omega * n)
display(Latex(r'$\large x[n] = |0.9|^n e^{j \frac{2\pi}{12} n} $'))
plt.figure(figsize=(14, 4))
plt.stem(n, np.real(exp_dec_sin), use_line_collection=True)
plt.xlabel('$n$')
plt.xticks(list(n)) # para graficar todos los números del eje x
plt.ylabel(r'$\Re \{ x[n] \}$');
$\large x[n] = |0.9|^n e^{j \frac{2\pi}{12} n} $

n = np.arange(31)
Omega = 2*np.pi/8
exp_dec_sin = (np.abs(1.1)**n)*np.exp(1j * Omega * n)
display(Latex(r'$\large x[n] = |1.1|^n e^{j (\frac{2\pi}{8}) n}$'))
plt.figure(figsize=(14, 4))
plt.stem(n, np.real(exp_dec_sin), use_line_collection=True)
plt.xlabel('$n$')
plt.xticks(list(n)) # para graficar todos los números del eje x
plt.ylabel(r'$\Re \{ x[n] \}$');
$\large x[n] = |1.1|^n e^{j (\frac{2\pi}{8}) n}$

Diferencias
Así como las similitudes entre las señales exponenciales y senoidales continuas y discretas son evidentes, las diferencias que existen entre ellas pueden pasar inadvertidas pero son muy importantes.
Para la señal continua $\large x(t) = e^{j \omega t}$:
Mientras mayor sea $\omega$, mayor sera la velocidad de oscilacion de la señal (mayor frecuencia).
$\large e^{j \omega_{0} t}$ Es periódica para cualquier valor de $\large \omega_{0}$.
Hay diferencias entre la version continua y discreta
Respecto a la frecuencia de oscilación
La señal exponencial Compleja discreta $\large x[n] = e^{j \omega n}$ con $ frecuencia = \omega_{0} + 2\pi$ \begin{equation} \large e^{j(\omega_{0}+2\pi)n} = e^{ j \omega_{0} n}e^{j 2\pi} = e^{j\omega_{0} n} \end{equation}
En el caso continuo las señales $e^{j \omega_{0} t}$ son distintas para distintos valores de $\omega_{0}$.
En el caso discreto la señal es identica para $\omega_{0} \pm 2\pi, : \omega_{0} \pm 4\pi, : …$ entonces al considerar las señales discretas exponenciales complejas solo se debe tomar en cuenta un intervalo de frecuencia de longitud de $2\pi$ dentro del cual se escoge $\omega_{0}$ puede ser: $0 \leq \omega_{0} < 2\pi :$ o este $:-\pi \leq \omega_{0} < \pi$
Debido a esta periodicidad, la velocidad de oscilación no tiene un incremento continuo con $\omega$, sino que incrementando $\omega$ a partir de cero, la velocidad de oscilación se va incrementando hasta que $\omega=\pi$, momento en el que empieza a disminuir hasta llegar a $\omega=2\pi$, que produce la misma señal que $\omega=0$. Por lo tanto, la señal exponencial discreta será de baja frecuencia si $\omega$ es próxima a 0 o un múltiplo par de $\pm \pi$. Y será de alta frecuencia si $\omega$ es próxima a un número impar de veces $\pm \pi$.
En concreto, para $\large \omega = \pi \rightarrow :: x[n] = e^{j\pi n} = (e^{j\pi})^n = (-1)^n$, oscilando de signo cada elemento.
Respecto a la periodicidad
Para que la señal exponencial discreta sea periódica con $periodo > N$, debe cumplirse que: \begin{equation} \large e^{j\omega_{0} n} = e^{j\omega_{0} (n+N)} = e^{j\omega_{0} n}e^{j\omega_{0} N} \ \large \rightarrow e^{j \omega_{0} N} = 1 \end{equation}
Para que esto se cumpla $\large e^{j \omega_{0} N}$ debe ser multiplo de $2\pi$ esto es que exista un entero $m \in \mathbb{Z}$ que cumpla: \begin{equation} \large \omega_{0} N = 2 \pi m \rightarrow \frac{\omega_{0}}{2\pi} = \frac{m}{N} \end{equation}
La señal es periodica si $\frac{m}{N}$ es un racional y es no periodica en otras circunstancias.
Usando los cálculos se puede determinar el periodo y la frecuencia de la señal discreta exponencial compleja. Si $x[n]$ es periodica con periodo fundamental $N$, su frecuencia fundamental es $\frac{2 \pi}{N}$.
El periodo fundamental es $\large N = m \left ( \frac{2 \pi}{\omega_{0}} \right )$
Resumen de las diferencias
| $\large x(t) = e^{j \omega_{0} t}$ | $\large x[n] = e^{j \omega_{0} n}$ |
|---|---|
| Señales diferentes para cada $\omega_{0}$ | Señales identicas para $\omega_{0}$ cada $m 2 \pi$ |
| Periodica para Cualquier $\omega_{0}$ | Periodica solo si $\large \omega_{0} = m (\frac{2 \pi}{N}) :N>0, m \in \mathbb{Z} $ |
| Frecuencia fundamental $\omega_{0}$ | Frecuencia fundamental $\large \frac{\omega_{0}}{m}$ |
| Periodo fundamental $T$ $\omega_{0} = 0 \rightarrow indefinido$ $\large \omega_{0} \neq 0 \rightarrow \frac{2 \pi}{\omega_{0}}$ | Periodo fundamental $N$ $\omega_{0} = 0 \rightarrow indefinido$ $\large \omega_{0} \neq 0 \rightarrow m \left (\frac{2 \pi}{\omega_{0}} \right )$ |
Ejemplos de Periodicidad
$\large x(t) = \cos(\frac{2 \pi t}{14})$ $\rightarrow$ Periodo = 14
$\large x[n] = \cos(\frac{2 \pi n}{14})$ $\rightarrow$ Periodo = 14
t = sym.symbols('t', real=True)
x1 = sym.cos((2*sym.pi/14) * t)
sym.plot(x1, (t, 0, 10*sym.pi), ylabel=r'$x(t)$',
title=r'$x(t) = \cos \left(\frac{2 \pi t}{14} \right)$', legend=True);

n = np.arange(31)
Omega = 2*np.pi/14
xn = np.cos(Omega * n)
plt.figure(figsize=(14, 4))
plt.stem(n, xn, use_line_collection=True)
plt.xlabel('$n$')
plt.xticks(list(n)) # para graficar todos los números del eje x
plt.title(r'$x[n] = \cos \left(\frac{2 \pi n}{14} \right)$')
plt.ylabel(r'$ x[n]$');

$\large x(t) = \cos(\frac{8 \pi t}{31})$ $\rightarrow$ periodo = $\frac{31}{4}$
$\large x[n] = \cos(\frac{8 \pi n}{31})$ $\rightarrow$ periodo = 31
t = sym.symbols('t', real=True)
x1 = sym.cos((8*sym.pi/31) * t)
sym.plot(x1, (t, 0, 6*sym.pi), ylabel=r'$x(t)$',
title=r'$x(t) = \cos \left(\frac{8 \pi t}{31} \right)$', legend=True);

n = np.arange(45)
Omega = 8*np.pi/31
xn = np.cos(Omega * n)
plt.figure(figsize=(14, 4))
plt.stem(n, xn, use_line_collection=True)
plt.xlabel('$n$')
plt.xticks(list(n)) # para graficar todos los números del eje x
plt.title(r'$x[n] = \cos(\frac{8 \pi n}{31})$')
plt.ylabel(r'$ x[n]$');

$\large x(t) = \cos(\frac{t}{6})$ $\rightarrow$ Periodo = $12 \pi$
$\large x[n] = \cos(\frac{n}{6})$ No es periodica, ningun numero entero es multiplo de $12 \pi$
t = sym.symbols('t', real=True)
x1 = sym.cos((1/6) * t)
sym.plot(x1, (t, 0, 27*sym.pi), ylabel=r'$x(t)$',
title=r'$x(t) = \cos(\frac{t}{6})$', legend=True);

n = np.arange(45)
Omega = 1/6
xn = np.cos(Omega * n)
plt.figure(figsize=(15, 4))
plt.stem(n, xn, use_line_collection=True)
plt.xlabel('$n$')
plt.xticks(list(n)) # para graficar todos los números del eje x
# para agregar los valores de cada punto
for a, b in zip(n, xn):
plt.text(a, b, str(b)[:4])
plt.title(r'$x[n] = \cos(\frac{n}{6})$')
plt.ylabel(r'$ x[n]$');

Periodo en Suma o Multiplicación de señales
Cuando tenemos una Multiplicación o suma de señales el peridodo sera el periodo comun entre las dos señales.
Por ejemplo si tenemos una señal $x_{1}(t)$ con periodo = 6 y otra señal $x_{2}(t)$ con periodo = 4 , entonces si estas dos señales se suman o se multiplican su periodo sera igual al minimo comun multiplo entre estos dos periodos que en este caso seria = 12.
Frecuencia Fundamental y Armonicos
Al igual que en el caso continuo en las señales periodicas discretars existen señales armonicas con periodo comun $N$, donde las frecuencias son multiplos de $\large \frac{2 \pi}{N}$ entonces: \begin{equation} \large \phi_{k}[n]=e^{j k \left( \frac{2 \pi}{N} \right)n} ::::: \text{para} ::::K=0, \pm1, \pm2, \pm3, … \end{equation}
En el caso de las señales continuas todas son distintas, pero en el caso discreto \begin{equation} \large \phi_{k+N}[n] = e^{j (k+N) \left( \frac{2 \pi}{N} \right)n} \rightarrow \ \large = e^{j k \left( \frac{2 \pi}{N} \right)n}e^{j 2 \pi n} = \phi_{k}[n] \end{equation}
Solo hay $N$ exponenciales periodicas diferentes: \begin{equation} \phi_{0}[n]= 1, \phi_{1}[n]=e^{j \left( \frac{2 \pi}{N} \right)n}, \phi_{2}[n]=e^{j \left( \frac{4 \pi}{N} \right)n}, : … : , \phi_{N-1}[n]=e^{j (N-1) \left( \frac{2 \pi}{N} \right)n} \end{equation} Las otras seran iguales.
- La frecuencia fundamental es cuando k = 1
- Las frecuencias armonicas son los multiplos enteros de la Fundamental
REFERENCIAS
Oppenheim Seccion 1.4
Phd. Jose R. Zapata
