Por Jose R. Zapata
Ultima actualizacion: 8/Dic/2023
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
print(pd.__version__)
1.5.3
información del dataset
información completa del dataset: https://raw.githubusercontent.com/jbrownlee/Datasets/master/auto_imports.names
Este conjunto de datos consta de tres tipos de caracteristicas:
- (a) la especificación de un automóvil en términos de diversas características
- (b) su calificación de riesgo de seguro asignada
- (c) sus pérdidas normalizadas en uso en comparación con otros automoviles.
La segunda calificación corresponde al grado en que el automovil es más riesgoso de lo que indica su precio.
Inicialmente, a los automóviles se les asigna un símbolo de factor de riesgo asociado con su precio. Luego, si es más arriesgado (o menos), este símbolo se ajusta moviéndolo hacia arriba (o hacia abajo) en la escala. Los actuarios llaman a este proceso “symboling”. Un valor de 3 indica que el automóvil es riesgoso, -3 que probablemente sea bastante seguro.
El tercer factor es el pago medio relativo por pérdida por año de vehículo asegurado. Este valor está normalizado para todos los automóviles dentro de una clasificación de tamaño particular (two-door small, station wagons, sports/speciality, etc…) y representa la pérdida promedio por automóvil por año.
La información del dataset describe que Los valores faltantes estan definidos con un “?”.
columnas = ['symboling', 'normalized-losses', 'make',
'fuel-type', 'aspiration', 'num-of-doors',
'body-style', 'drive-wheels', 'engine-location',
'wheel-base', 'length', 'width', 'height',
'curb-weight', 'engine-type', 'num-of-cylinders',
'engine-size', 'fuel-system', 'bore', 'stroke',
'compression-ratio', 'horsepower', 'peak-rpm',
'city-mpg', 'highway-mpg', 'price']
url_data = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/auto_imports.csv'
auto_df = pd.read_csv(url_data,
header=None,
names=columnas,
na_values='?')
# Ver 5 registros aleatorios
auto_df.sample(5)
| symboling | normalized-losses | make | fuel-type | aspiration | num-of-doors | body-style | drive-wheels | engine-location | wheel-base | ... | engine-size | fuel-system | bore | stroke | compression-ratio | horsepower | peak-rpm | city-mpg | highway-mpg | price | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 79 | 3 | NaN | mitsubishi | gas | turbo | two | hatchback | fwd | front | 95.9 | ... | 156 | spdi | 3.58 | 3.86 | 7.0 | 145.0 | 5000.0 | 19 | 24 | 12629 |
| 64 | -1 | 93.0 | mercedes-benz | diesel | turbo | four | sedan | rwd | front | 110.0 | ... | 183 | idi | 3.58 | 3.64 | 21.5 | 123.0 | 4350.0 | 22 | 25 | 25552 |
| 163 | 2 | 134.0 | toyota | gas | std | two | hardtop | rwd | front | 98.4 | ... | 146 | mpfi | 3.62 | 3.50 | 9.3 | 116.0 | 4800.0 | 24 | 30 | 8449 |
| 54 | 3 | 150.0 | mazda | gas | std | two | hatchback | rwd | front | 95.3 | ... | 70 | 4bbl | NaN | NaN | 9.4 | 101.0 | 6000.0 | 17 | 23 | 13645 |
| 78 | 3 | 153.0 | mitsubishi | gas | std | two | hatchback | fwd | front | 96.3 | ... | 122 | 2bbl | 3.35 | 3.46 | 8.5 | 88.0 | 5000.0 | 25 | 32 | 8499 |
5 rows × 26 columns
#Tamaño del dataset
auto_df.shape
(201, 26)
auto_df.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 201 entries, 0 to 200
Data columns (total 26 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 symboling 201 non-null int64
1 normalized-losses 164 non-null float64
2 make 201 non-null object
3 fuel-type 201 non-null object
4 aspiration 201 non-null object
5 num-of-doors 199 non-null object
6 body-style 201 non-null object
7 drive-wheels 201 non-null object
8 engine-location 201 non-null object
9 wheel-base 201 non-null float64
10 length 201 non-null float64
11 width 201 non-null float64
12 height 201 non-null float64
13 curb-weight 201 non-null int64
14 engine-type 201 non-null object
15 num-of-cylinders 201 non-null object
16 engine-size 201 non-null int64
17 fuel-system 201 non-null object
18 bore 197 non-null float64
19 stroke 197 non-null float64
20 compression-ratio 201 non-null float64
21 horsepower 199 non-null float64
22 peak-rpm 199 non-null float64
23 city-mpg 201 non-null int64
24 highway-mpg 201 non-null int64
25 price 201 non-null int64
dtypes: float64(10), int64(6), object(10)
memory usage: 41.0+ KB
Preparacion del dataset
Datos faltantes
Los datos fueron cargados reemplazando los simbolos “?” como valores faltantes, como estaba definido en la información del dataset.
auto_df.isna().sum()
symboling 0
normalized-losses 37
make 0
fuel-type 0
aspiration 0
num-of-doors 2
body-style 0
drive-wheels 0
engine-location 0
wheel-base 0
length 0
width 0
height 0
curb-weight 0
engine-type 0
num-of-cylinders 0
engine-size 0
fuel-system 0
bore 4
stroke 4
compression-ratio 0
horsepower 2
peak-rpm 2
city-mpg 0
highway-mpg 0
price 0
dtype: int64
Convertir las variables a su formato correcto
en base a la información del dataset, se convierten las variables a su formato correcto.
Corregir las variables categoricas
cols_categoricas = ["make", "fuel-type", "aspiration", "num-of-doors",
"body-style", "drive-wheels", "engine-location",
"engine-type", "num-of-cylinders", "fuel-system"]
auto_df[cols_categoricas] = auto_df[cols_categoricas].astype("category")
Corregir variables categorica ordinal
auto_df["num-of-doors"] = pd.Categorical(auto_df["num-of-doors"],
categories=["two","four"],
ordered=True)
auto_df["num-of-cylinders"] = pd.Categorical(auto_df["num-of-cylinders"],
categories=["two", "three", "four",
"five", "six", "eight",
"twelve"],
ordered=True)
información del dataset
auto_df.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 201 entries, 0 to 200
Data columns (total 26 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 symboling 201 non-null int64
1 normalized-losses 164 non-null float64
2 make 201 non-null category
3 fuel-type 201 non-null category
4 aspiration 201 non-null category
5 num-of-doors 199 non-null category
6 body-style 201 non-null category
7 drive-wheels 201 non-null category
8 engine-location 201 non-null category
9 wheel-base 201 non-null float64
10 length 201 non-null float64
11 width 201 non-null float64
12 height 201 non-null float64
13 curb-weight 201 non-null int64
14 engine-type 201 non-null category
15 num-of-cylinders 201 non-null category
16 engine-size 201 non-null int64
17 fuel-system 201 non-null category
18 bore 197 non-null float64
19 stroke 197 non-null float64
20 compression-ratio 201 non-null float64
21 horsepower 199 non-null float64
22 peak-rpm 199 non-null float64
23 city-mpg 201 non-null int64
24 highway-mpg 201 non-null int64
25 price 201 non-null int64
dtypes: category(10), float64(10), int64(6)
memory usage: 29.7 KB
Descripcion estadistica
auto_df.describe()
| symboling | normalized-losses | wheel-base | length | width | height | curb-weight | engine-size | bore | stroke | compression-ratio | horsepower | peak-rpm | city-mpg | highway-mpg | price | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| count | 201.000000 | 164.000000 | 201.000000 | 201.000000 | 201.000000 | 201.000000 | 201.000000 | 201.000000 | 197.000000 | 197.000000 | 201.000000 | 199.000000 | 199.000000 | 201.000000 | 201.000000 | 201.000000 |
| mean | 0.840796 | 122.000000 | 98.797015 | 174.200995 | 65.889055 | 53.766667 | 2555.666667 | 126.875622 | 3.330711 | 3.256904 | 10.164279 | 103.396985 | 5117.587940 | 25.179104 | 30.686567 | 13207.129353 |
| std | 1.254802 | 35.442168 | 6.066366 | 12.322175 | 2.101471 | 2.447822 | 517.296727 | 41.546834 | 0.270793 | 0.319256 | 4.004965 | 37.553843 | 480.521824 | 6.423220 | 6.815150 | 7947.066342 |
| min | -2.000000 | 65.000000 | 86.600000 | 141.100000 | 60.300000 | 47.800000 | 1488.000000 | 61.000000 | 2.540000 | 2.070000 | 7.000000 | 48.000000 | 4150.000000 | 13.000000 | 16.000000 | 5118.000000 |
| 25% | 0.000000 | 94.000000 | 94.500000 | 166.800000 | 64.100000 | 52.000000 | 2169.000000 | 98.000000 | 3.150000 | 3.110000 | 8.600000 | 70.000000 | 4800.000000 | 19.000000 | 25.000000 | 7775.000000 |
| 50% | 1.000000 | 115.000000 | 97.000000 | 173.200000 | 65.500000 | 54.100000 | 2414.000000 | 120.000000 | 3.310000 | 3.290000 | 9.000000 | 95.000000 | 5200.000000 | 24.000000 | 30.000000 | 10295.000000 |
| 75% | 2.000000 | 150.000000 | 102.400000 | 183.500000 | 66.600000 | 55.500000 | 2926.000000 | 141.000000 | 3.590000 | 3.410000 | 9.400000 | 116.000000 | 5500.000000 | 30.000000 | 34.000000 | 16500.000000 |
| max | 3.000000 | 256.000000 | 120.900000 | 208.100000 | 72.000000 | 59.800000 | 4066.000000 | 326.000000 | 3.940000 | 4.170000 | 23.000000 | 262.000000 | 6600.000000 | 49.000000 | 54.000000 | 45400.000000 |
auto_df.head()
| symboling | normalized-losses | make | fuel-type | aspiration | num-of-doors | body-style | drive-wheels | engine-location | wheel-base | ... | engine-size | fuel-system | bore | stroke | compression-ratio | horsepower | peak-rpm | city-mpg | highway-mpg | price | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 3 | NaN | alfa-romero | gas | std | two | convertible | rwd | front | 88.6 | ... | 130 | mpfi | 3.47 | 2.68 | 9.0 | 111.0 | 5000.0 | 21 | 27 | 13495 |
| 1 | 3 | NaN | alfa-romero | gas | std | two | convertible | rwd | front | 88.6 | ... | 130 | mpfi | 3.47 | 2.68 | 9.0 | 111.0 | 5000.0 | 21 | 27 | 16500 |
| 2 | 1 | NaN | alfa-romero | gas | std | two | hatchback | rwd | front | 94.5 | ... | 152 | mpfi | 2.68 | 3.47 | 9.0 | 154.0 | 5000.0 | 19 | 26 | 16500 |
| 3 | 2 | 164.0 | audi | gas | std | four | sedan | fwd | front | 99.8 | ... | 109 | mpfi | 3.19 | 3.40 | 10.0 | 102.0 | 5500.0 | 24 | 30 | 13950 |
| 4 | 2 | 164.0 | audi | gas | std | four | sedan | 4wd | front | 99.4 | ... | 136 | mpfi | 3.19 | 3.40 | 8.0 | 115.0 | 5500.0 | 18 | 22 | 17450 |
5 rows × 26 columns
auto_df.to_parquet('automobile_processed.parquet',
index=False)
análisis Univariable
Se debe hacer un análisis de cada una de las variables y describir sus caracteristicas.
Realizar el análisis univarible es muy importante para entender el comportamiento de cada una de las variables y poder detectar posibles problemas en los datos. Nunca saltarse este paso.
El enfasis de este capitulo es el proceso de Regresion con Scikit-learn entonces previamente se analizaron cada una de las variables. Solo se hara enfasis en unas variables que se consideran importantes para el proceso de regresion.
cols_categoricas
['make',
'fuel-type',
'aspiration',
'num-of-doors',
'body-style',
'drive-wheels',
'engine-location',
'engine-type',
'num-of-cylinders',
'fuel-system']
cols_cate_problemas = ["make", "fuel-system", "num-of-cylinders"]
for col in cols_cate_problemas:
print(auto_df[col].value_counts())
print("")
toyota 32
nissan 18
mazda 17
mitsubishi 13
honda 13
volkswagen 12
subaru 12
peugot 11
volvo 11
dodge 9
mercedes-benz 8
bmw 8
plymouth 7
audi 6
saab 6
porsche 4
jaguar 3
chevrolet 3
alfa-romero 3
isuzu 2
renault 2
mercury 1
Name: make, dtype: int64
mpfi 92
2bbl 64
idi 20
1bbl 11
spdi 9
4bbl 3
mfi 1
spfi 1
Name: fuel-system, dtype: int64
four 157
six 24
five 10
two 4
eight 4
three 1
twelve 1
Name: num-of-cylinders, dtype: int64
Algunos valores categoricos solo estan presentes en un solo registro, por ejemplo solo hay un registro con el valor “mercury” en la variable “make”, por lo que lleva a problemas en los encoders. otros registros con este problema son:
make = mercury, fuel-system = mfi o spfi , num-of-cylinders = three o twelve
Una solucion es agregar en el feature engineering la opcion de manejar cuando se presenten estos casos. (Se peude perder conocimiento de los datos que se estan respondiendo con el modelo) Se toma esta solucion
Otra solucion es tomar estos registros y garantizar que siempre esten en el conjunto de entrenamiento. este procedimiento necesita un desarrollo mas complejo.
cond_1 = "`fuel-system` in ['mfi', 'spfi']"
cond_2 = "`num-of-cylinders` in ['three', 'twelve']"
cond_3 = "make == 'mercury'"
auto_df.query(f"{cond_1} | {cond_2} | {cond_3}")
| symboling | normalized-losses | make | fuel-type | aspiration | num-of-doors | body-style | drive-wheels | engine-location | wheel-base | ... | engine-size | fuel-system | bore | stroke | compression-ratio | horsepower | peak-rpm | city-mpg | highway-mpg | price | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 17 | 2 | 121.0 | chevrolet | gas | std | two | hatchback | fwd | front | 88.4 | ... | 61 | 2bbl | 2.91 | 3.03 | 9.5 | 48.0 | 5100.0 | 47 | 53 | 5151 |
| 28 | 3 | 145.0 | dodge | gas | turbo | two | hatchback | fwd | front | 95.9 | ... | 156 | mfi | 3.60 | 3.90 | 7.0 | 145.0 | 5000.0 | 19 | 24 | 12964 |
| 43 | 2 | NaN | isuzu | gas | std | two | hatchback | rwd | front | 96.0 | ... | 119 | spfi | 3.43 | 3.23 | 9.2 | 90.0 | 5000.0 | 24 | 29 | 11048 |
| 46 | 0 | NaN | jaguar | gas | std | two | sedan | rwd | front | 102.0 | ... | 326 | mpfi | 3.54 | 2.76 | 11.5 | 262.0 | 5000.0 | 13 | 17 | 36000 |
| 72 | 1 | NaN | mercury | gas | turbo | two | hatchback | rwd | front | 102.7 | ... | 140 | mpfi | 3.78 | 3.12 | 8.0 | 175.0 | 5000.0 | 19 | 24 | 16503 |
5 rows × 26 columns
análisis Bivariable
Scatter Plots
#listado de variables numericas excepto price
cols_numericas = (auto_df
.drop(columns=["price"])
.select_dtypes(include=np.number)
.columns.tolist())
cols_numericas
['symboling',
'normalized-losses',
'wheel-base',
'length',
'width',
'height',
'curb-weight',
'engine-size',
'bore',
'stroke',
'compression-ratio',
'horsepower',
'peak-rpm',
'city-mpg',
'highway-mpg']
len(cols_numericas)
15
# son 15 variables numericas
# el plot seran 5 filas y 3 columnas
fig, axes = plt.subplots(5, 3, figsize=(15, 15))
axes = axes.flatten()
for i, col in enumerate(cols_numericas):
sns.regplot(data=auto_df,
x=col, y="price",
ax=axes[i])
axes[i].set_title(col)
plt.tight_layout()
plt.show()
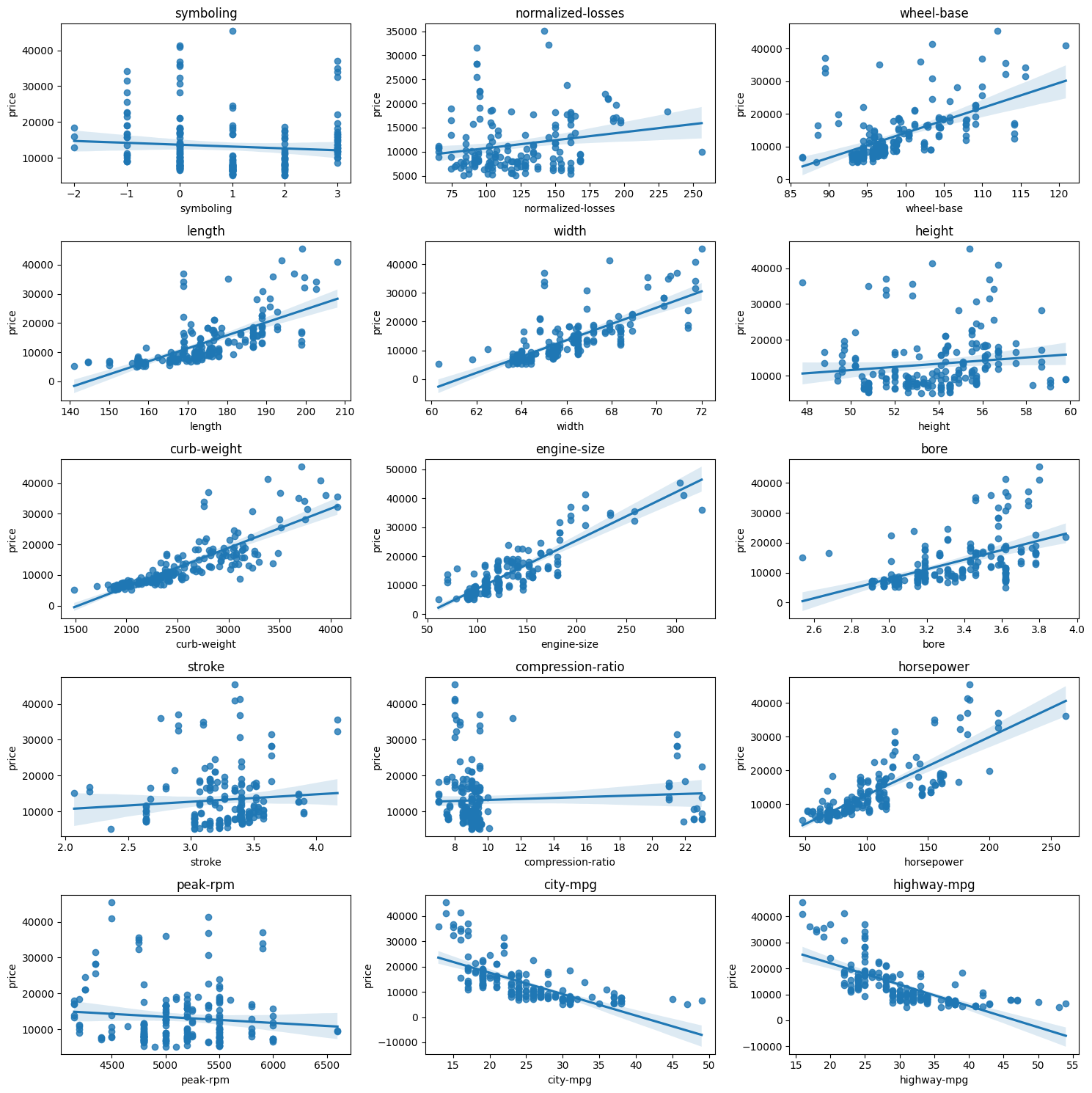
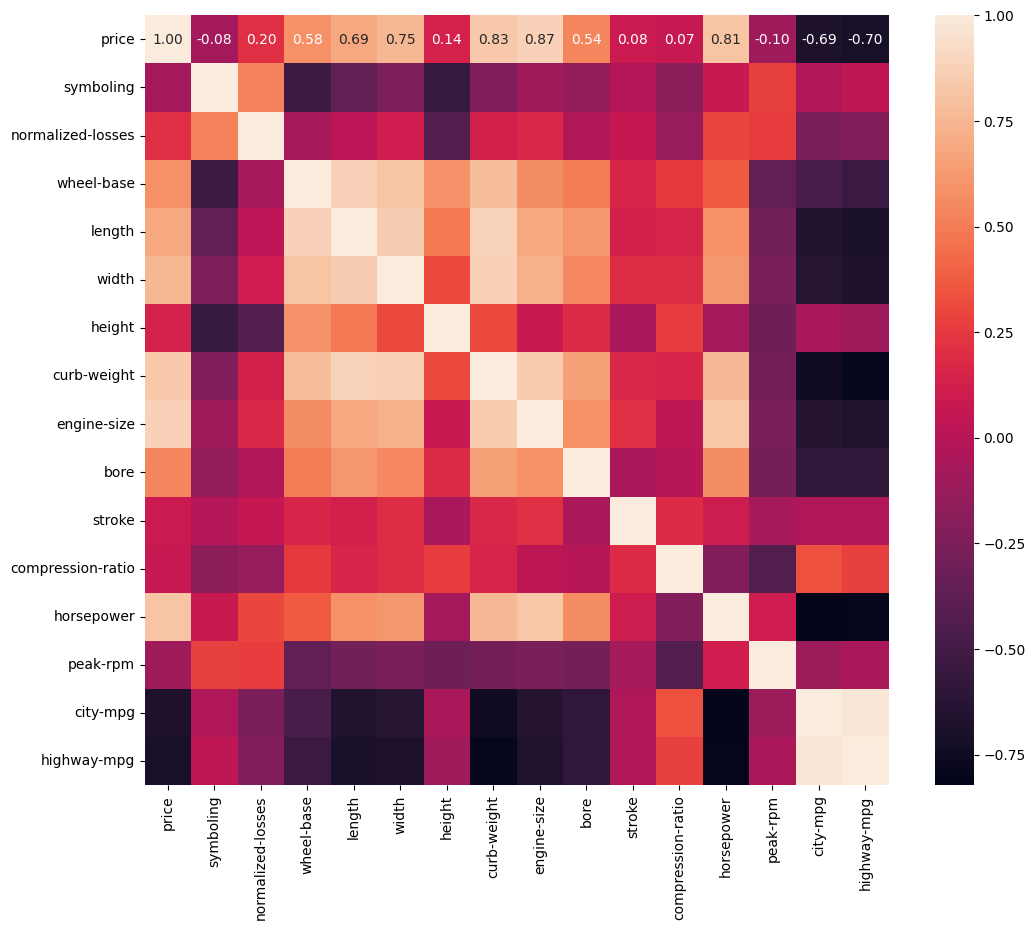
Correlacion
Visualizar la correlacion entre las variables numericas, es importante recordar que La correlación de Pearson es una medida estadística que se utiliza para cuantificar la relación lineal entre dos variables continuas, y estas variables continuas deben ser lineales.
Visualmente se puede ver en las graficas de scatter plots anteriormente presentadas. por ejemplo:
- la variable
engine-sizeypricetienen una relacion lineal positiva. - por el contrario la variable
symbolingypriceno tienen una relacion lineal, entonces el valor de la correlacion de pearson no es valido.
# mover la columna price al inicio en el dataframe auto_df
# para que los valores de correlacion se vean al inicio
cols = auto_df.columns.tolist()
cols.insert(0, cols.pop(cols.index("price")))
auto_df = auto_df.reindex(columns= cols)
automobile_corr = auto_df.corr(numeric_only=True)
fig, ax = plt.subplots(figsize=(12, 10))
sns.heatmap(automobile_corr, annot=True, fmt=".2f");
Visualizacion variables categoricas
len(cols_categoricas)
10
# son 15 variables numericas
# el plot seran 5 filas y 3 columnas
fig, axes = plt.subplots(5, 2, figsize=(15, 15))
axes = axes.flatten()
for i, col in enumerate(cols_categoricas):
sns.boxplot(data=auto_df,
x="price", y=col,
ax=axes[i])
axes[i].set_title(col)
plt.tight_layout()
plt.show()
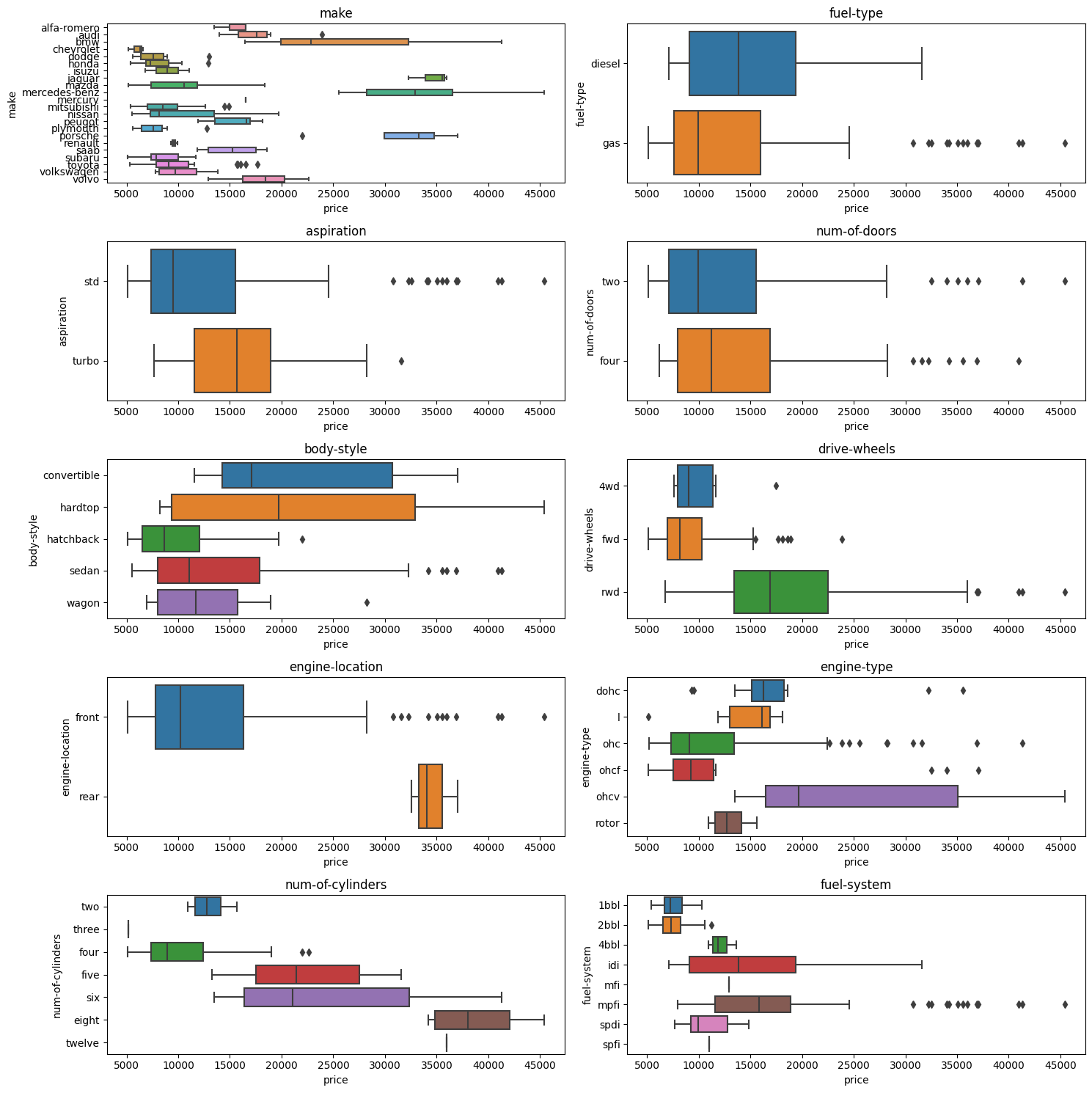
Hay variables categoricas que permiten distinguir entre grupos de valores de la variable objetivo, por ejemplo la variable engine-location los dos boxplots tienen una diferencia significativa, por lo que es una variable que aporta información al modelo.
La variable num-of-doors no permite distinguir entre grupos de valores de la variable objetivo price, por lo que no es una variable que aporte información al modelo la distribuccion de los boxplots son similares.
para medir la relacion entre variables categoricas y la variable objetivo que es numerica se puede usar la prueba de ANOVA.
Feature Engineering (Ingenieria de caracteristicas)
Se va realizar una imputacion simple sin tener en cuenta un análisis mas profundo de los datos y la distribucion de los mismos.
las variables numericas se imputaran con la media y las variables categoricas con la moda.
# librerias para el preprocesamiento de datos
from sklearn.pipeline import Pipeline
from sklearn.impute import SimpleImputer
from sklearn.preprocessing import OrdinalEncoder
from sklearn.preprocessing import OneHotEncoder
from sklearn.compose import ColumnTransformer
cols_numericas = ['symboling','normalized-losses',
'wheel-base','length', 'width',
'height', 'curb-weight',
'engine-size', 'bore', 'stroke',
'compression-ratio', 'horsepower',
'peak-rpm','city-mpg',
'highway-mpg']
cols_categoricas = ["make", "fuel-type", "aspiration",
"body-style", "drive-wheels",
"engine-location", "engine-type",
"fuel-system"]
cols_categoricas_ord = [ "num-of-doors", "num-of-cylinders"]
Creacion de pipelines de transformacion, la codificacion es:
OneHotEncoderpara las variables categoricas nominalesOrdinalEncoderpara las variables categoricas ordinales
numeric_pipe = Pipeline(steps=[
('imputer', SimpleImputer(strategy='median'))])
categorical_pipe = Pipeline(steps=[
('imputer', SimpleImputer(strategy='most_frequent')),
('onehot', OneHotEncoder(handle_unknown='ignore'))])
categorical_ord_pipe = Pipeline(steps=[
('ordenc', OrdinalEncoder(handle_unknown='use_encoded_value',
unknown_value=np.nan)),
('imputer', SimpleImputer(strategy='most_frequent'))])
preprocessor = ColumnTransformer(
transformers=[
('numericas', numeric_pipe, cols_numericas),
('categoricas', categorical_pipe, cols_categoricas),
('categoricas ordinales', categorical_ord_pipe, cols_categoricas_ord)
])
preprocessor
ColumnTransformer(transformers=[('numericas',
Pipeline(steps=[('imputer',
SimpleImputer(strategy='median'))]),
['symboling', 'normalized-losses',
'wheel-base', 'length', 'width', 'height',
'curb-weight', 'engine-size', 'bore',
'stroke', 'compression-ratio', 'horsepower',
'peak-rpm', 'city-mpg', 'highway-mpg']),
('categoricas',
Pipeline(steps=[('imputer',
SimpleImputer...
OneHotEncoder(handle_unknown='ignore'))]),
['make', 'fuel-type', 'aspiration',
'body-style', 'drive-wheels',
'engine-location', 'engine-type',
'fuel-system']),
('categoricas ordinales',
Pipeline(steps=[('ordenc',
OrdinalEncoder(handle_unknown='use_encoded_value',
unknown_value=nan)),
('imputer',
SimpleImputer(strategy='most_frequent'))]),
['num-of-doors', 'num-of-cylinders'])])In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
ColumnTransformer(transformers=[('numericas',
Pipeline(steps=[('imputer',
SimpleImputer(strategy='median'))]),
['symboling', 'normalized-losses',
'wheel-base', 'length', 'width', 'height',
'curb-weight', 'engine-size', 'bore',
'stroke', 'compression-ratio', 'horsepower',
'peak-rpm', 'city-mpg', 'highway-mpg']),
('categoricas',
Pipeline(steps=[('imputer',
SimpleImputer...
OneHotEncoder(handle_unknown='ignore'))]),
['make', 'fuel-type', 'aspiration',
'body-style', 'drive-wheels',
'engine-location', 'engine-type',
'fuel-system']),
('categoricas ordinales',
Pipeline(steps=[('ordenc',
OrdinalEncoder(handle_unknown='use_encoded_value',
unknown_value=nan)),
('imputer',
SimpleImputer(strategy='most_frequent'))]),
['num-of-doors', 'num-of-cylinders'])])['symboling', 'normalized-losses', 'wheel-base', 'length', 'width', 'height', 'curb-weight', 'engine-size', 'bore', 'stroke', 'compression-ratio', 'horsepower', 'peak-rpm', 'city-mpg', 'highway-mpg']
SimpleImputer(strategy='median')
['make', 'fuel-type', 'aspiration', 'body-style', 'drive-wheels', 'engine-location', 'engine-type', 'fuel-system']
SimpleImputer(strategy='most_frequent')
OneHotEncoder(handle_unknown='ignore')
['num-of-doors', 'num-of-cylinders']
OrdinalEncoder(handle_unknown='use_encoded_value', unknown_value=nan)
SimpleImputer(strategy='most_frequent')
Modelos de Regresion
Dividir el dataset en entrenamiento y prueba
from sklearn.model_selection import train_test_split
X_features = auto_df.drop('price', axis='columns')
Y_target = auto_df['price']
x_train, x_test, y_train, y_test = train_test_split(X_features,
Y_target,
test_size=0.2,
random_state=42)
x_train.shape, y_train.shape
((160, 25), (160,))
x_test.shape, y_test.shape
((41, 25), (41,))
Regresion modelo simple
Cross Validation modelo simple
Regresión con Múltiples Modelos
Si se tienen muchos modelos realizar cross validation con todos es costoso computacionalmente y en tiempo, entonces se debe ir descartando los modelos con menos desempeño hasta llegar al modelo final
- Inicialmente se dividen los datos en una parte para realizar la seleccion del modelo (Model selection dataset) y otra para realizar la prueba de desempeño (Performance dataset, esta parte de los datos se debe usar solo en el final de todo el proceso)
- Primer paso es dividir el Model selection dataset en una parte de entrenamiento (train) y otra de prueba (test), normalmente en una proporcion de 80/20 o 70/30.
- Hacer una evaluacion de todos los modelos la division enterior y seleccionar los mejores (preferiblemente que tengan un principio de funcionamiento diferente entre ellos).
- Con lo mejores modelos (la cantidad depende de que tan parecido es su resultado) realizar un cross-validation (detectar si hay over-fitting) para obtener los que tengan mejor resultado.
- Se saca el mejor o los mejores modelos (Los que tengan mejor desempeño y poca varianza en sus resultados) y se realiza optimizacion de hiper parametros (Hyper parameter Tunning). Este proceso es costoso computacionalmente por eso se debe realizar con muy pocos modelos.
- Luego se selecciona el mejor modelo (Mejor desempeño y poca varianza) y se obtienen los hiper parametros que dieron el mejor resultado.
- Finalmente se entrena el modelo seleccionado con los hiper-parametros hallados sobre el Model selection dataset y se hace la prueba final con el Performance dataset
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_absolute_error
from sklearn.dummy import DummyRegressor
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import Lasso
from sklearn.linear_model import Ridge
from sklearn.linear_model import ElasticNet
from sklearn.svm import SVR
from sklearn.neighbors import KNeighborsRegressor
from sklearn.tree import DecisionTreeRegressor
import warnings
warnings.filterwarnings("ignore")
result_dict = {}
FEATURES = list(x_train.columns)
FEATURES
['symboling',
'normalized-losses',
'make',
'fuel-type',
'aspiration',
'num-of-doors',
'body-style',
'drive-wheels',
'engine-location',
'wheel-base',
'length',
'width',
'height',
'curb-weight',
'engine-type',
'num-of-cylinders',
'engine-size',
'fuel-system',
'bore',
'stroke',
'compression-ratio',
'horsepower',
'peak-rpm',
'city-mpg',
'highway-mpg']
funciones de ayuda
def entrenar_modelo(modelo,
preprocessor: ColumnTransformer,
x_data: pd.DataFrame,
y_data: pd.Series,
test_frac:float=0.2,
):
"""entrenar_modelo
función para entrenar y evaluar un modelo
Args:
modelo (scikit-learn model ): modelo de ML
preprocessor (ColumnTransformer): preprocesador de datos
x_data (pd.DataFrame): datos de entrada
y_data (pd.Series): datos de salida
test_frac (float): fraccion de datos para el conjunto de prueba
Returns:
dict: diccionario con los puntajes de entrenamiento y prueba
"""
# dividir el dataset en entrenamiento y prueba
x_train, x_test, y_train, y_test = train_test_split(x_data, y_data,
random_state=42,
test_size=test_frac)
# crear el pipeline con el preprocesador y el modelo
regressor_pipe = Pipeline(steps=[("preprocessor", preprocessor),
("model", modelo)])
# entrenar el pipeline de regresion
model = regressor_pipe.fit(x_train, y_train)
y_pred_train = model.predict(x_train)
# predecir con el pipeline de regresion
y_pred = model.predict(x_test)
train_score = mean_absolute_error(y_train, y_pred_train)
test_score = mean_absolute_error(y_test, y_pred)
print("Entrenamiento_score : " , train_score)
print("Prueba_score : ", test_score)
return {
'Entrenamiento_score': train_score,
'Prueba_score': test_score
}
# función para comparar los resultados de los modelos
#se van a almacenar en un diccionario
def compare_results():
for key in result_dict:
print('Regresion: ', key)
print('Entrenamiento score', result_dict[key]['Entrenamiento_score'])
print('Prueba score', result_dict[key]['Prueba_score'])
print()
Modelos Simple
result_dict['Dummy Regressor'] = entrenar_modelo(DummyRegressor(strategy='median'),
preprocessor,
x_train,
y_train)
Entrenamiento_score : 4968.09375
Prueba_score : 4166.40625
Regresion lineal
result_dict['Linear Regressor'] = entrenar_modelo(LinearRegression(),
preprocessor,
x_train,
y_train)
Entrenamiento_score : 876.91871739725
Prueba_score : 2227.1959787155765
Lasso
result_dict['Lasso'] = entrenar_modelo(Lasso(alpha=0.5),
preprocessor,
x_train,
y_train)
Entrenamiento_score : 875.8499493696161
Prueba_score : 2073.4851183651135
compare_results()
Regresion: Dummy Regressor
Entrenamiento score 4968.09375
Prueba score 4166.40625
Regresion: Linear Regressor
Entrenamiento score 876.91871739725
Prueba score 2227.1959787155765
Regresion: Lasso
Entrenamiento score 875.8499493696161
Prueba score 2073.4851183651135
Ridge
result_dict['Ridge'] = entrenar_modelo(Ridge(alpha=0.5),
preprocessor,
x_train,
y_train)
Entrenamiento_score : 1013.8811988326221
Prueba_score : 1686.5907495083325
Elasticnet
result_dict['Elasticnet'] = entrenar_modelo(ElasticNet(alpha=1, l1_ratio=0.5,
max_iter= 100000,
warm_start= True),
preprocessor,
x_train,
y_train)
Entrenamiento_score : 1823.047871927852
Prueba_score : 2033.2624431034096
SVR
For SVR regression with larger datasets this alternate implementations is preferred
https://scikit-learn.org/stable/modules/generated/sklearn.svm.LinearSVR.html#sklearn.svm.LinearSVR
- Uses a different library for implementation
- More flexibility with choice of penalties
- Scales to larger datasets
result_dict['SVR'] = entrenar_modelo(SVR(kernel='linear',
epsilon=0.05,
C=0.3),
preprocessor,
x_train,
y_train)
Entrenamiento_score : 1973.1475811870937
Prueba_score : 2084.487575544151
KNR
result_dict['KNR'] = entrenar_modelo(KNeighborsRegressor(n_neighbors=10),
preprocessor,
x_train,
y_train)
Entrenamiento_score : 2319.37421875
Prueba_score : 1686.978125
Decision Tree
result_dict['Decision Tree'] = entrenar_modelo(DecisionTreeRegressor(max_depth=2),
preprocessor,
x_train,
y_train)
Entrenamiento_score : 2095.9670005416547
Prueba_score : 2354.1148396002236
compare_results()
Regresion: Dummy Regressor
Entrenamiento score 4968.09375
Prueba score 4166.40625
Regresion: Linear Regressor
Entrenamiento score 876.91871739725
Prueba score 2227.1959787155765
Regresion: Lasso
Entrenamiento score 875.8499493696161
Prueba score 2073.4851183651135
Regresion: Ridge
Entrenamiento score 1013.8811988326221
Prueba score 1686.5907495083325
Regresion: Elasticnet
Entrenamiento score 1823.047871927852
Prueba score 2033.2624431034096
Regresion: SVR
Entrenamiento score 1973.1475811870937
Prueba score 2084.487575544151
Regresion: KNR
Entrenamiento score 2319.37421875
Prueba score 1686.978125
Regresion: Decision Tree
Entrenamiento score 2095.9670005416547
Prueba score 2354.1148396002236
# Crear un diccionario solo con los resultados de prueba de cada modelo
nombre_modelos = result_dict.keys()
resultados_train = {} # crear diccionario vacio
resultados_test = {} # crear diccionario vacio
for nombre in nombre_modelos:
resultados_train[nombre] = result_dict[nombre]['Entrenamiento_score']
resultados_test[nombre] = result_dict[nombre]['Prueba_score']
df_comparacion = pd.DataFrame([resultados_train, resultados_test],
index=['train', 'test'])
# Plot the bar chart
fig, ax = plt.subplots(figsize=(10, 4))
df_comparacion.T.plot(kind='bar', ax=ax)
# Adjust the layout
ax.set_ylabel('MAE score')
ax.set_title('Comparacion de Modelos [MAE] ')
# Set the x-tick labels inside the bars and rotate by 90 degrees
ax.set_xticks(range(len(df_comparacion.columns)))
ax.set_xticklabels([])
# Draw the x-tick labels inside the bars rotated by 90 degrees
for i, label in enumerate(df_comparacion.columns):
bar_center = (df_comparacion.loc['train', label] +
df_comparacion.loc['test', label]) / 2
ax.text(i, bar_center, label, ha='center',
va='center_baseline', rotation=45)
#plot line at DUmmerRegressor result
ax.axhline(df_comparacion['Dummy Regressor']['test'],
color='red',
linestyle='--',
alpha=0.8)
plt.tight_layout()
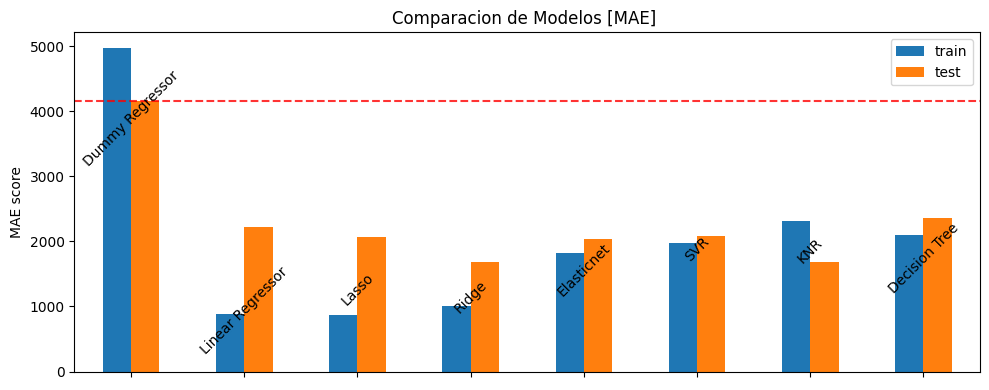
Cross Validation - Seleccion de Modelos
Analizar la varianza de los resultados para obtener los que tengan mejor resultado.
# lista para almacenar cada uno los modelos seleccionados para el cross validation
models = []
# Alamcenando los modelos como una tupla (nombre, modelo)
models.append(('LinearRegression',LinearRegression()))
models.append(('Lasso',Lasso(alpha=0.5)))
models.append(('Elastic_net',ElasticNet(alpha=1,
l1_ratio=0.5,
max_iter= 100000,
warm_start= True)))
models.append(('Kneighbors',KNeighborsRegressor(n_neighbors=10)))
models.append(('Decision_tree',DecisionTreeRegressor(max_depth=2)))
models.append(('SVR',SVR(kernel='linear', epsilon=0.05, C=0.3)))
# Grabar los resultados de cada modelo
from sklearn import model_selection
#Semilla para obtener los mismos resultados de pruebas
seed = 2
results = []
names = []
scoring = 'neg_mean_absolute_error'
for name, model in models:
# Kfold cross validation for model selection
kfold = model_selection.KFold(n_splits=10)
model_pipe = Pipeline(steps=[("preprocessor", preprocessor),
("model", model)])
#X train , y train
cv_results = model_selection.cross_val_score(model_pipe, x_train, y_train,
cv=kfold, scoring=scoring)
# la metrica neg_mean_absolute_error se debe convertir en positiva
cv_results = np.abs(cv_results)
results.append(cv_results)
names.append(name)
msg = f"({name}, {cv_results.mean()}, {cv_results.std()}"
print(msg)
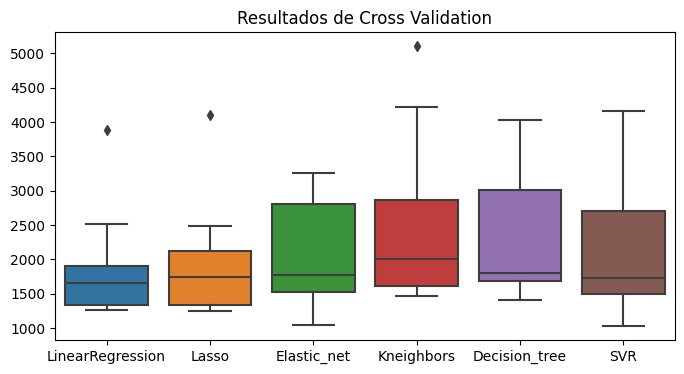
(LinearRegression, 1880.4279376299269, 759.7083856523359
(Lasso, 1942.3275850979167, 819.8989669274982
(Elastic_net, 2064.237025880098, 748.8943233081599
(Kneighbors, 2537.4762499999997, 1178.6072239843625
(Decision_tree, 2361.6768311488745, 904.4913144311246
(SVR, 2153.3895318330706, 1045.9967491538698
plt.figure(figsize = (8,4))
result_df = pd.DataFrame(results, index=names).T
sns.boxplot(data=result_df)
plt.title("Resultados de Cross Validation")
plt.show()
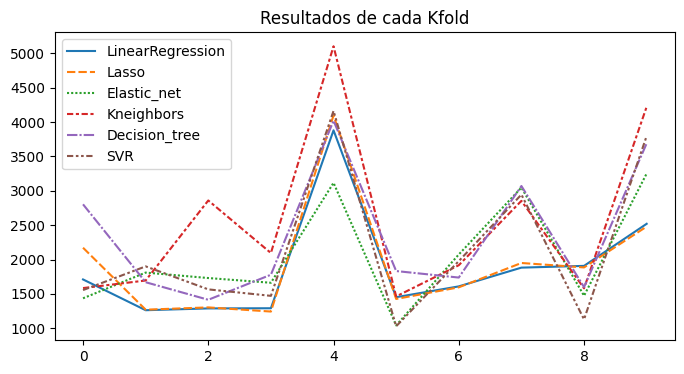
plt.figure(figsize = (8,4))
sns.lineplot(data=result_df)
plt.title("Resultados de cada Kfold")
plt.show()
Comparacion Estadistica de Modelos
from scipy.stats import f_oneway
model1 = result_df['LinearRegression']
model2 = result_df['Lasso']
model3 = result_df['Elastic_net']
model4 = result_df['Kneighbors']
model5 = result_df['Decision_tree']
model6 = result_df['SVR']
statistic, p_value = f_oneway(model1, model2, model3, model4, model5, model6)
print(f'Statistic: {statistic}')
print(f'p_value: {p_value}')
alpha = 0.05 # nivel de significancia
if p_value < alpha:
print("Existe una diferencia estadísticamente "
"significativa en los resultados de"
" cross-validation de los modelos.")
else:
print("No Existe una diferencia estadísticamente "
"significativa en los resultados de "
"cross-validation de los modelos.")
Statistic: 0.671567588915147
p_value: 0.6467064865579687
No Existe una diferencia estadísticamentesignificativa en los resultados de cross-validation de los modelos.
Hyper Parameter Tunning
Optimizacion de hiperparametros, Se seleccionan los mejores modelos que tengan diferente formas de funcionamiento.
from sklearn.model_selection import GridSearchCV
Lasso regression
parameters = {'model__alpha': [0.2, 0.4, 0.6, 0.7, 0.8, 0.9, 1.0]}
lasso_pipe = Pipeline(steps=[("preprocessor", preprocessor),
("model", Lasso())])
grid_search = GridSearchCV(lasso_pipe, parameters, cv=5,
return_train_score=True,
scoring='neg_mean_absolute_error')
grid_search.fit(x_train, y_train);
Resultados de la hiperparametrizacion
# la medida neg_mean_absolute_error se debe convertir en positiva
print(f"Mejor resultado = {abs(grid_search.best_score_)}")
print(f"Mejor std = {grid_search.cv_results_['std_test_score'][grid_search.best_index_]}")
print(f"Mejor parametros = {grid_search.best_params_}")
Mejor resultado = 1947.2883893277037
Mejor std = 395.70957523074117
Mejor parametros = {'model__alpha': 1.0}
# Para ver todos los resultados del cross validation
# No es necesario, solo es informativo para ver como varia el modelo
for i in range(len(parameters['model__alpha'])):
print('Parametros: ', grid_search.cv_results_['params'][i])
print('Promedio Score Prueba: ', np.abs(grid_search
.cv_results_['mean_test_score'][i]))
print('Std Score Prueba: ', grid_search.cv_results_['std_test_score'][i])
print('Rank: ', grid_search.cv_results_['rank_test_score'][i])
Parametros: {'model__alpha': 0.2}
Promedio Score Prueba: 2010.296312054496
Std Score Prueba: 428.9844282221353
Rank: 7
Parametros: {'model__alpha': 0.4}
Promedio Score Prueba: 1992.2295569543373
Std Score Prueba: 413.26837036444175
Rank: 6
Parametros: {'model__alpha': 0.6}
Promedio Score Prueba: 1975.7918087502098
Std Score Prueba: 403.8384726869151
Rank: 5
Parametros: {'model__alpha': 0.7}
Promedio Score Prueba: 1969.570409045271
Std Score Prueba: 402.4853958339954
Rank: 4
Parametros: {'model__alpha': 0.8}
Promedio Score Prueba: 1962.48783429974
Std Score Prueba: 400.28336690299744
Rank: 3
Parametros: {'model__alpha': 0.9}
Promedio Score Prueba: 1955.014676715969
Std Score Prueba: 397.6643201093387
Rank: 2
Parametros: {'model__alpha': 1.0}
Promedio Score Prueba: 1947.2883893277037
Std Score Prueba: 395.70957523074117
Rank: 1
grid_search.best_params_
{'model__alpha': 1.0}
lasso_pipe = Pipeline(steps=[("preprocessor", preprocessor),
("model", Lasso(alpha=grid_search
.best_params_['model__alpha']))])
lasso_model = lasso_pipe.fit(x_train, y_train)
y_pred = lasso_model.predict(x_test)
y_pred_train = lasso_model.predict(x_train)
print('Entrenamiento score: ', mean_absolute_error(y_train, y_pred_train))
print('Prueba score: ', mean_absolute_error(y_test, y_pred))
Entrenamiento score: 1004.6129068520986
Prueba score: 1618.7963705622894
KNeighbors regression
parameters = {'model__n_neighbors': [10, 12, 14, 18, 20, 25, 30, 35, 50]}
knn_pipe = Pipeline(steps=[("preprocessor", preprocessor),
("model", KNeighborsRegressor())])
grid_search = GridSearchCV(knn_pipe, parameters, cv=5,
return_train_score=True,
scoring='neg_mean_absolute_error')
grid_search.fit(x_train, y_train);
print(f"Mejor resultado = {abs(grid_search.best_score_)}")
print(f"Mejor std = {grid_search.cv_results_['std_test_score'][grid_search.best_index_]}")
print(f"Mejor parametros = {grid_search.best_params_}")
Mejor resultado = 2403.674652777778
Mejor std = 606.3296590961176
Mejor parametros = {'model__n_neighbors': 18}
knn_pipe = Pipeline(steps=[("preprocessor", preprocessor),
("model", KNeighborsRegressor(n_neighbors=grid_search.
best_params_['model__n_neighbors']))])
kneighbors_model = knn_pipe.fit(x_train, y_train)
y_pred = kneighbors_model.predict(x_test)
y_pred_train = kneighbors_model.predict(x_train)
print('Entrenamiento score: ', mean_absolute_error(y_train, y_pred_train))
print('Prueba score: ', mean_absolute_error(y_test, y_pred))
Entrenamiento score: 2262.2024305555556
Prueba score: 4446.5609756097565
Decision Tree
parameters = {'model__max_depth': [4, 5, 7, 9, 10],
'model__max_features': [5, 10, 15, 20,30],
'model__criterion': ['squared_error',
'absolute_error',
'poisson',
'friedman_mse'],
}
dt_pipe = Pipeline(steps=[("preprocessor", preprocessor),
("model", DecisionTreeRegressor())])
grid_search = GridSearchCV(dt_pipe, parameters, cv=5,
scoring='neg_mean_absolute_error',
return_train_score=True)
grid_search.fit(x_train, y_train);
print(f"Mejor resultado = {abs(grid_search.best_score_)}")
print(f"Mejor std = {grid_search.cv_results_['std_test_score'][grid_search.best_index_]}")
print(f"Mejor parametros = {grid_search.best_params_}")
Mejor resultado = 1826.1523958333332
Mejor std = 297.55591804730403
Mejor parametros = {'model__criterion': 'poisson', 'model__max_depth': 10, 'model__max_features': 30}
model = DecisionTreeRegressor(max_depth=grid_search.best_params_['model__max_depth'],
criterion=grid_search.best_params_['model__criterion'])
dt_pipe = Pipeline(steps=[("preprocessor", preprocessor),
("model",model)])
decision_tree_model = dt_pipe.fit(x_train, y_train)
y_pred = decision_tree_model.predict(x_test)
y_pred_train = decision_tree_model.predict(x_train)
print('Entrenamiento score: ', mean_absolute_error(y_train, y_pred_train))
print('Prueba score: ', mean_absolute_error(y_test, y_pred))
Entrenamiento score: 245.96577380952377
Prueba score: 2183.026713124274
Esta diferencia entre entrenamiento y prueba se debe a que el modelo esta sobreajustado (overfitt), es decir, esta memorizando los datos de entrenamiento y no generaliza bien para los datos de prueba.
Este fenomeno se puede reducir con la regularizacion, en este caso con el parametro min_samples_leaf que indica el numero minimo de muestras que debe tener una hoja para que el modelo no siga creciendo. pero como se tienen pocos datos, no se va continuar con este modelo.
SVR
parameters = {'model__epsilon': [0.05, 0.1, 0.2, 0.3],
'model__C': [0.2, 0.3]}
svr_pipe = Pipeline(steps=[("preprocessor", preprocessor),
("model", SVR(kernel='linear'))])
grid_search = GridSearchCV(svr_pipe, parameters, cv=5,
scoring='neg_mean_absolute_error',
return_train_score=True)
grid_search.fit(x_train, y_train);
print(f"Mejor resultado = {abs(grid_search.best_score_)}")
print(f"Mejor std = {grid_search.cv_results_['std_test_score'][grid_search.best_index_]}")
print(f"Mejor parametros = {grid_search.best_params_}")
Mejor resultado = 2123.62832932766
Mejor std = 438.3741180824112
Mejor parametros = {'model__C': 0.3, 'model__epsilon': 0.05}
model = SVR(kernel='linear',
epsilon=grid_search.best_params_['model__epsilon'],
C=grid_search.best_params_['model__C'])
svr_pipe = Pipeline(steps=[("preprocessor", preprocessor),
("model", model)])
svr_model = svr_pipe.fit(x_train, y_train)
y_pred = svr_model.predict(x_test)
y_pred_train = svr_model.predict(x_train)
print('Entrenamiento score: ', mean_absolute_error(y_train, y_pred_train))
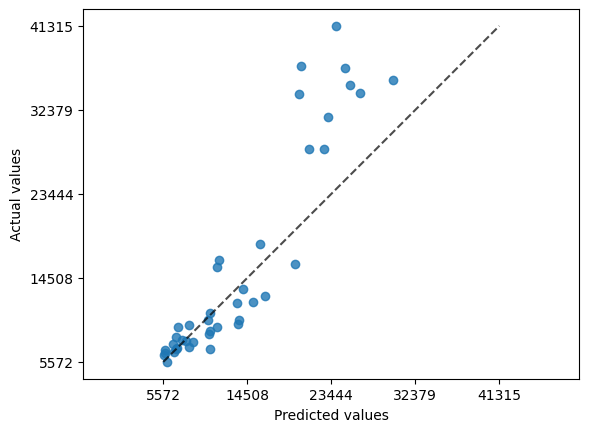
print('Prueba score: ', mean_absolute_error(y_test, y_pred))
Entrenamiento score: 1986.9969013172886
Prueba score: 3829.808694217932
from sklearn.metrics import PredictionErrorDisplay
PredictionErrorDisplay.from_predictions(y_true=y_test,
y_pred=y_pred,
kind="actual_vs_predicted");
PredictionErrorDisplay.from_predictions(y_true=y_test,
y_pred=y_pred,
kind="residual_vs_predicted");
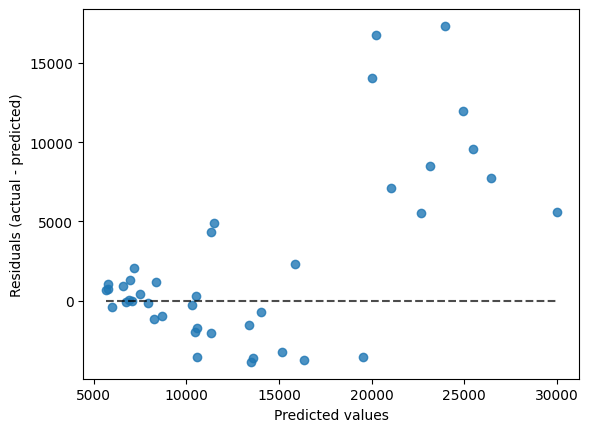
Interpretacion del Modelo
Como mejor modelo se selecciona el SVR, con el siguientes parametros:
{'C': 0.3, 'epsilon': 0.05}
from sklearn.inspection import permutation_importance
imps = permutation_importance(svr_pipe, x_test, y_test,
n_repeats = 5,
scoring= "neg_mean_absolute_error",
n_jobs=-1, random_state=42)
fig= plt.figure(figsize=(10,8))
perm_sorted_idx = imps.importances_mean.argsort()
plt.boxplot(imps.importances[perm_sorted_idx].T, vert=False,
labels=x_test.columns[perm_sorted_idx])
plt.title("Permutation Importances (test set)");
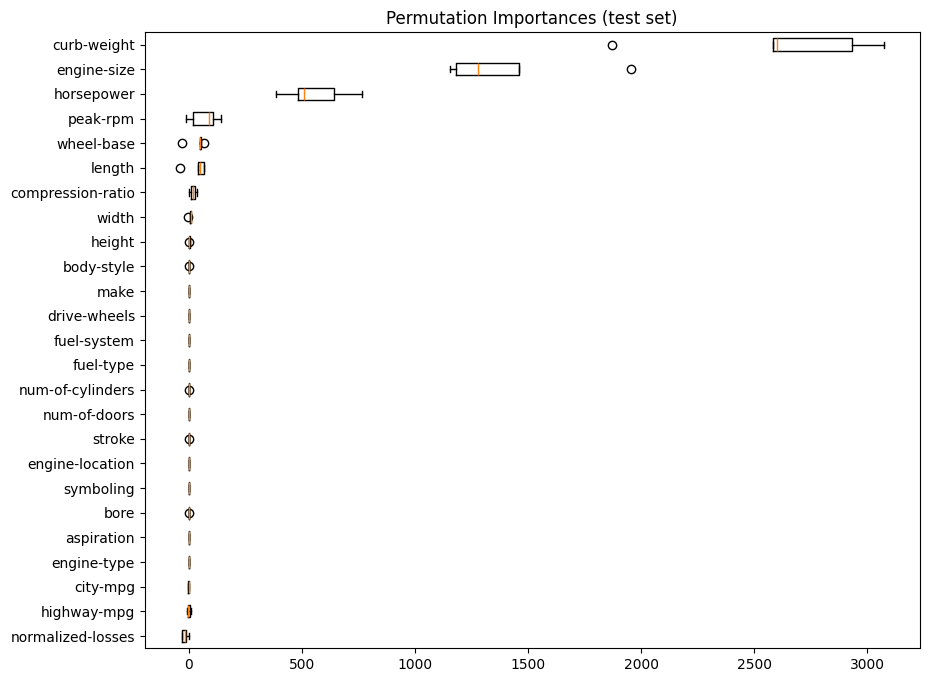
En base a estos resultados se pueden reducir el numero de variables y obtener un modelo mas simple con mas o menos el mismo desempeño.
viendo las graficas solo tomare las 8 variables mas importantes.
#los valores estan en orden ascendente, entonces se deben tomar los ultimos 8
# se puede comprobar al comparar con el grafico de barras
cols_seleccionadas = x_test.columns[perm_sorted_idx][-8:].tolist()
cols_seleccionadas
['width',
'compression-ratio',
'length',
'wheel-base',
'peak-rpm',
'horsepower',
'engine-size',
'curb-weight']
Modelo con menos variables
x_train = x_train[cols_seleccionadas]
x_test = x_test[cols_seleccionadas]
x_train.head()
| width | compression-ratio | length | wheel-base | peak-rpm | horsepower | engine-size | curb-weight | |
|---|---|---|---|---|---|---|---|---|
| 198 | 68.9 | 8.8 | 188.8 | 109.1 | 5500.0 | 134.0 | 173 | 3012 |
| 38 | 65.2 | 9.0 | 175.4 | 96.5 | 5800.0 | 86.0 | 110 | 2304 |
| 24 | 63.8 | 9.4 | 157.3 | 93.7 | 5500.0 | 68.0 | 90 | 1989 |
| 122 | 68.3 | 9.5 | 168.9 | 94.5 | 5500.0 | 143.0 | 151 | 2778 |
| 196 | 68.9 | 9.5 | 188.8 | 109.1 | 5400.0 | 114.0 | 141 | 2952 |
todas son variables numericas, por lo que se debe modificar el pipeline de transformacion.
preprocessor = Pipeline(steps=[
('imputer', SimpleImputer(strategy='median'))])
model = SVR(kernel='linear',
epsilon=0.05,
C=0.3)
svr_pipe = Pipeline(steps=[("preprocessor", preprocessor),
("model", model)])
svr_model = svr_pipe.fit(x_train, y_train)
y_pred = svr_model.predict(x_test)
y_pred_train = svr_model.predict(x_train)
print('Entrenamiento score: ', mean_absolute_error(y_train, y_pred_train))
print('Prueba score: ', mean_absolute_error(y_test, y_pred))
Entrenamiento score: 2002.511781975918
Prueba score: 3821.046214783602
El resultado anterior fue:
Entrenamiento score: 1986.9969013172886
Prueba score: 3829.808694217932
los resultados son muy similares, por lo que se puede tomar este modelo con menos variables.
Procesamiento y Modelo Final con scikit-learn
Luego realizar la seleccion del modelo final y sus hiperparametros, se procede a crear un pipeline completo de entrenamiento con todos los datos y prediccion.
En un proceso de Ciencia de datos se debe entrenar con todos los datos disponibles si es posible, para que el modelo final tenga la mayor cantidad de información posible. lo que evita que el modelo final tenga sobreajuste son los hiperparametros que se optimizaron en el paso anterior. Esto se hace en la aplicaciones reales, ya que normalmente los datos se van actualizando, por ejemplo en un sistema de clasificacion de anomalias, el modelo se va actualizando con los nuevos datos que van surgiendo y se va reentrenando con los datos historicos(pasado), para predecir datos presentes y futuros.
En este caso se va a usar el modelo de SVR con los hiperparametros
{'C': 0.3, 'epsilon': 0.05}
Pipeline Final
Para entrenar el pipeline final se leen los datos limpios, solamente las columnas definidas anteriormente
columnas = ['width', 'compression-ratio', 'length',
'wheel-base', 'peak-rpm', 'horsepower',
'engine-size', 'price']
url_data = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/auto_imports.csv'
auto_df = pd.read_csv(url_data,
header=None,
names=columnas,
na_values='?')
se dividen los datos en las variables de entrada y la variable de salida
X = auto_df.drop('price', axis='columns')
y = auto_df['price']
Se entrena el ultimo pipeline con todos los datos
svr_model = svr_pipe.fit(X, y)
Grabar el Modelo
Se Selecciona el modelo que obtuvo mejores resultados en la hiperparametrizacion y sus resultados eran buenos con el dataset de prueba (test)
from joblib import dump# libreria de serializacion
# grabar el modelo en un archivo
dump(svr_model, 'svr_model-auto.joblib')
['svr_model-auto.joblib']
Usar el Modelo
import pandas as pd
from joblib import load
modelo = load('svr_model-auto.joblib')
modelo
Pipeline(steps=[('preprocessor',
Pipeline(steps=[('imputer',
SimpleImputer(strategy='median'))])),
('model', SVR(C=0.3, epsilon=0.05, kernel='linear'))])In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
Pipeline(steps=[('preprocessor',
Pipeline(steps=[('imputer',
SimpleImputer(strategy='median'))])),
('model', SVR(C=0.3, epsilon=0.05, kernel='linear'))])Pipeline(steps=[('imputer', SimpleImputer(strategy='median'))])SimpleImputer(strategy='median')
SVR(C=0.3, epsilon=0.05, kernel='linear')
# tomar dos datos de entrada para realizar la prediccion, eliminando la columna precio
datos_prueba = X. sample(2)
datos_prueba
| width | compression-ratio | length | wheel-base | peak-rpm | horsepower | engine-size | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| -1 | 74.0 | volvo | gas | std | four | wagon | rwd | front | 104.3 | 188.8 | 67.2 | 57.5 | 3034 | ohc | four | 141 | mpfi | 3.78 | 3.15 | 9.5 | 114.0 | 5400.0 | 23 | 28 |
| 1 | 128.0 | nissan | gas | std | two | sedan | fwd | front | 94.5 | 165.3 | 63.8 | 54.5 | 1889 | ohc | four | 97 | 2bbl | 3.15 | 3.29 | 9.4 | 69.0 | 5200.0 | 31 | 37 |
# resultados de predicion con el modelo
modelo.predict(datos_prueba)
array([13048.35343294, 7295.61626863])
Phd. Jose R. Zapata
