Phd. Jose R. Zapata

Las Ondas acusticas es el que se transmite a través del aire como oscilaciones de presión de aire. En esencia, el sonido es simplemente vibración del aire.

El Sonido se refiere a la producción, transmisión o recepción de sonidos audibles por los humanos. Una señal de audio es una representación digital del sonido que representa la fluctuación en la presión del aire causada por la vibración en función del tiempo. A diferencia de las partituras o las representaciones simbólicas, las representaciones de audio codifican todo lo que es necesario para reproducir un sonido.

Señales de audio en python

Lectura y reproducción de archivos de audio
Visualización de señales de audio
Escribir archivos de audio

Librerias de Python para análisis de audio

Scipy (scipy.signal, scipy.fftpack, scipy.io )
Librosa (https://librosa.org/)
PyAudioAnalysis (https://github.com/tyiannak/pyAudioAnalysis)
Essentia (http://essentia.upf.edu)
Madmon (https://github.com/CPJKU/madmom)
OpenSmile (https://audeering.com/technology/opensmile/)

Manejo de Audio Python

Python tiene incluido varios modulos para usar archivos de audio, pero son librerias muy basicas

audioop : Manipular datos de audio en bruto(raw)
wave : Leer y escribir archivos WAV
sndhdr : Determinar el tipo de archivo de audio

Escuchar sonidos en Jupyter Notebook

import IPython.display as ipd # Para reproducir audio en el Jupyter Notebook
#Crear una sinusoidal artificial y escucharla
import numpy as np
sr = 22050 # Frecuencia de Muestreo
T = 3.0    # segundos
t = np.linspace(0, T, int(T*sr), endpoint=False) # Variable de tiempo
x = 0.5*np.sin(2*np.pi*440*t)                # Sinusoidal pura a 440 Hz
ipd.Audio(x, rate=sr) # Escuchar el array Numpy

Representacion en el Tiempo

Libreria scipy.io

Es un ecosistema en Python de software de código abierto para Matemáticas, ciencia y ingeniería. En particular, estos son algunos de los paquetes principales:

Leer Audio

#Importar Modulo scipy para leer y grabar audio
from scipy.io import wavfile
AudioName = "Whistle.wav" # Archivo de Audio

# Salida fs: Frecuencia de muestreo and data: Señal de audio -> int16
fs, Audiodata = wavfile.read(AudioName)
print(f'Duracion = {Audiodata.shape[0]/fs} , Frecuencia de Muestreo = {fs} [=] Muestras/Seg' \
      f', Wav format = {Audiodata.dtype}')

ipd.Audio(AudioName) # Reproduce el audio directamente en el Jupyter notebook.

Duracion = 3.1887981859410433 , Frecuencia de Muestreo = 44100 [=] Muestras/Seg, Wav format = int16

Visualizar la Señal de Audio

import matplotlib.pyplot as plt #Libreria para realizar graficos

plt.rcParams['figure.figsize'] = (15, 5) # Definir el tamaño de graficas
plt.plot(Audiodata) # Audiodata es un numpy array
plt.text(0-5000, np.max(Audiodata), 'Máximo', fontsize = 16,bbox=dict(facecolor='red', alpha=0.5))
plt.title('Señal de Audio sin valores adecuados en los ejes',size=16);

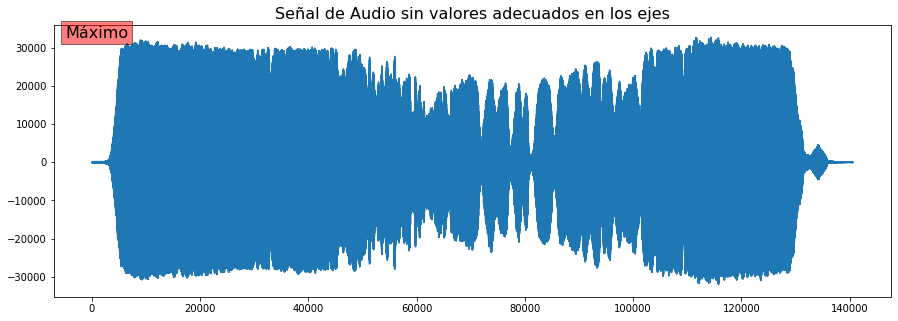
Definir los ejes adecuados

Las Señales de Audio se representan con la amplitud entre -1 y 1 , y el eje Horizontal en tiempo

# Importar Numpy para realizar operaciones en el vector de audio
import numpy as np

plt.rcParams['figure.figsize'] = (15, 5) # Definir el tamaño de graficas
# Definir los valores de los datos de amplitud entre [-1 : 1] Audiodata.dtype es int16
AudiodataScaled = Audiodata/(2**15)

#definir los valores del eje x en milisegundos
timeValues = np.arange(0, len(AudiodataScaled), 1)/ fs # Convertir Muestras/Seg a Segundos
timeValues = timeValues * 1000  #Escala de tiempo en milisegundos

plt.plot(timeValues, AudiodataScaled);plt.title('Señal de Audio Con información de Ejes',size=16)
plt.text(0-100, np.max(AudiodataScaled), 'Máximo', fontsize = 16,bbox=dict(facecolor='red', alpha=0.5))
plt.ylabel('Amplitud'); plt.xlabel('Tiempo (ms)');

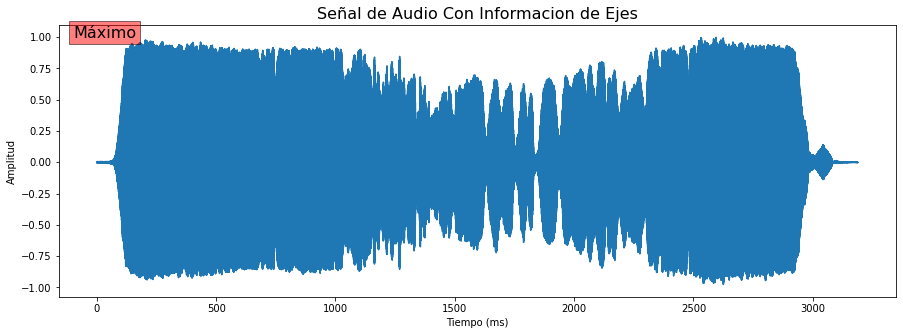
Grabar Archivos de Audio

Grabar a INT 16

# Realizando algunos cambios en la señal de audio original
LessGaindata = AudiodataScaled/2.0 # Dividiendo por dos la amplitud de la señal

# Convertir nuevamente la señal a int16 patra gabar el archivo a 16 Bits @ 441000 Hz
LessGaindataInt = LessGaindata*(2.**15)
LessGaindataInt = LessGaindataInt.astype(np.int16)

wavfile.write('LessGainInt.wav',fs,LessGaindataInt)

Grabar a Float

## Se graba en formato float point cuando no se indica nada

# Escribir la señal de audio a un archivo
wavfile.write('LessGainFloat.wav',fs,LessGaindata)

# La ventaja es: La amplitud del archivo de audio estara entre [-1 : 1]
# Entonces cuadno se lee el archivo de audio ya estara bien el eje vertical

#Leer los archivos de audio grabados
fs1, FileInt = wavfile.read('LessGainInt.wav')
fs2, FileFloat = wavfile.read('LessGainFloat.wav')

plt.subplot(121)
plt.plot(timeValues,FileInt);plt.title('Señal de audio Int transformada',size=16)
plt.ylabel('Amplitud'); plt.xlabel('Tiempo (ms)');
plt.subplot(122)
plt.plot(timeValues,FileFloat);plt.title('Señal de audio Float transformada',size=16)
plt.ylabel('Amplitud'); plt.xlabel('Tiempo (ms)');

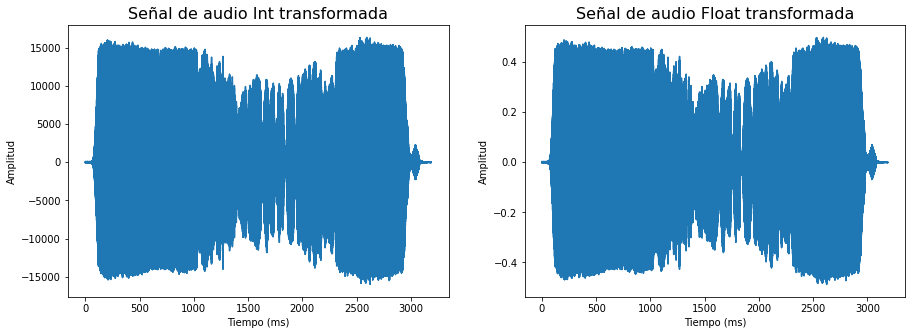
Libreria Librosa

Libreria para procesamiento de audio y musica en python, https://librosa.org/ La instalacion puede ser:

Anaconda: conda install -c conda-forge librosa
Pip: pip install librosa

Ademas para leer archivos con compresion: conda install -c conda-forge ffmpeg

Las computadoras digitales solo pueden capturar estos datos en momentos discretos. La velocidad a la que una computadora captura datos de audio se denomina frecuencia de muestreo (a menudo abreviado fs) o tasa de muestreo (a menudo abreviadosr).La frecuencia de muestreo de las grabaciones de CD es de 44100 Hz a 16 bits.

fs = frequency sample
sr = sample rate

Leer archivos de audio

import librosa # importar a libreria librosa
print(f'Version de Librosa: {librosa.__version__}')
x, sr = librosa.load('Data/Whistle.wav',sr=None)
#Si no se especifica sr=None, entonces el audio se cambia de sampling a 22050
# automaticamente carga el audio como un float
print(f'Tamaño del archivo de audio = {x.shape}, Frecuencia de Muestreo = {sr} y tipo de dato = {x.dtype}')

Version de Librosa: 0.7.1
Tamaño del archivo de audio = (140626,), Frecuencia de Muestreo = 44100 y tipo de dato = float32

Visualizar la señal de Audio

El cambio en la presión del aire en un momento determinado se representa gráficamente mediante un gráfico de presión-tiempo, o simplemente forma de onda.

import matplotlib.pyplot as plt
import librosa.display
plt.figure(figsize=(14, 5))
librosa.display.waveplot(x, sr=sr); plt.title('Librosa configura los ejes automaticamente');

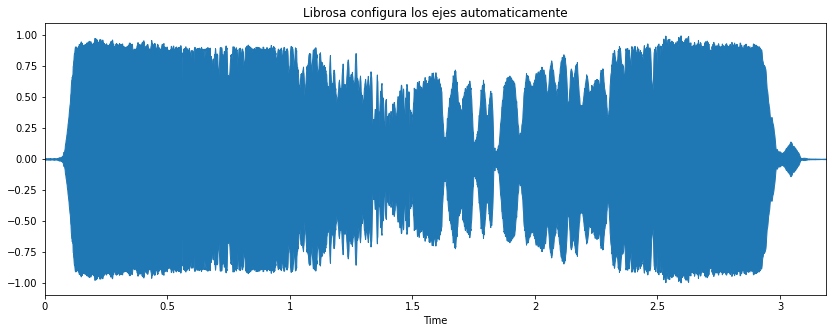
Grabar Archivo de Audio

se puede realizar con la libreria soundfile

sf.write Graba un arreglo NumPy como un archivo WAV.

import soundfile as sf
sf.write('Data/Librosa_audio.wav', x, sr)

Representacion en Frecuencia

Transformada Rapida de Fourier (FFT)
Espectro de magnitud(2D)
Espectrograma (3D)

fs, Audiodata = wavfile.read(AudioName) # Leer archivo de audio
Audiodata = Audiodata / (2.**15) # definir amplitud de los datos entre [-1 : 1]

from scipy.fftpack import fft # modulo para calcular la transformada de fourier
n = len(Audiodata)
AudioFreq = fft(Audiodata) # Calcular la transformada de Fourier
# La salida de la FFT es un array de números complejos
print(f'Tipo de datos de la fft = {AudioFreq.dtype} un valor cualquiera es = {AudioFreq[100]}')

Tipo de datos de la fft = complex128 un valor cualquiera es = (1.9588460421839156-0.10838638363682496j)

# La salida de la FFT es un array de números complejos
# los números complejos se representan en Magnitud y fase
MagFreq = np.abs(AudioFreq) # Valor absoluto para obtener la magnitud

# Escalar por el numero de puntos para evitar que los valores de magnitud
# dependan del tamaño de la señal o de su frecuencia de muestreo
MagFreq = MagFreq / float(n)

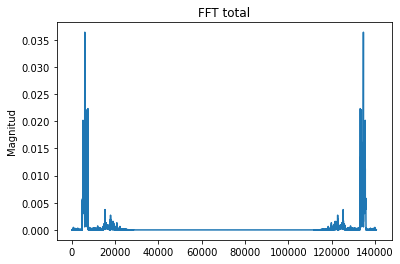
plt.plot(MagFreq) #Espectro de magnitud
plt.ylabel('Magnitud'); plt.title('FFT total');

Escala de Magnitud

A menudo, la amplitud original de una señal en el dominio de tiempo o de lafrecuencia no es perceptualmente relevante para los humanos como la amplitud convertida en otras unidades, Ej: usar una escala logarítmica.

Por ejemplo, consideremos un tono puro cuya amplitud aumenta de forma lineal. Definir la variable de tiempo:

T = 5.0      # duracion en segundos
sr = 22050   # Frecuencia de muestreo en Hz
t = np.linspace(0, T, int(T*sr), endpoint=False)

Crear una señal que su amplitud aumente linealmente

amplitude = np.linspace(0, 1, int(T*sr), endpoint=False) # Amplitud variable en el tiempo
x = amplitude*np.sin(2*np.pi*440*t) #Señal sinusoidal

ipd.Audio(x, rate=sr)

# Grafica de la señal:
librosa.display.waveplot(x, sr=sr);

Ahora considere una señal cuya amplitud crece exponencialmente, es decir, el logaritmo de la amplitud es lineal:

amplitude = np.logspace(-2, 0, int(T*sr), endpoint=False, base=10.0)
x = amplitude*np.sin(2*np.pi*440*t)

ipd.Audio(x, rate=sr)

librosa.display.waveplot(x, sr=sr);

A pesar de que la amplitud crece exponencialmente, para nosotros, el aumento en el volumen parece más gradual. Este fenómeno es un ejemplo de la ley Weber-Fechner law (Wikipedia)que establece que la relación entre un estímulo y la percepción humana es logarítmica.

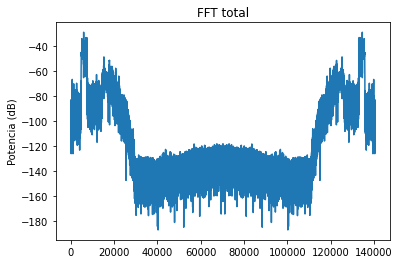
# Las señales se representan en el espectro de potencia
# las señales tienen comportamiento logaritmico

# Calcular el espectro de potencia
MagFreq = MagFreq**2
plt.plot(10*np.log10(MagFreq)) #Espectro de potencia
plt.ylabel('Potencia (dB)'); plt.title('FFT total');

AudioFreq = AudioFreq[0:int(np.ceil((n+1)/2.0))]
# La salida de la FFT es un array de números complejos
MagFreq = np.abs(AudioFreq) # Valor absoluto para obtener la magnitud

# Escalar por el numero de puntos para evitar que los valores de magnitud
# dependan del tamaño de la señal o de su frecuencia de muestreo
MagFreq = MagFreq / float(n)
# Calcular el espectro de potencia
MagFreq = MagFreq**2

Espectro de Magnitud (2D)

# Importar Plotly para realizar graficos interactivos
# conda install -c anaconda plotly
import plotly.express as px

# Verificar si nfft es impar para encontrar el punto de Nyquist en el espectro

if n % 2 > 0: # Si tenemos un numero impar de puntos de la fft
    MagFreq[1:len(MagFreq)] = MagFreq[1:len(MagFreq)] * 2
else:# Si tenemos un numero par de puntos de la fft
    MagFreq[1:len(MagFreq) -1] = MagFreq[1:len(MagFreq) - 1] * 2

freqAxis = np.arange(0,int(np.ceil((n+1)/2.0)), 1.0) * (fs / n);
fig = px.line(x = freqAxis/1000.0,
              y = 10*np.log10(MagFreq),
              title = 'Espectro Interactivo',
              labels={'x':'Frecuencia (kHz)', 'y':'Potencia (dB)'}
              ) #Espectro de potencia

## Solo por verificar una propiedad basica
# El valor RMS de la señal de audio en el tiempo
# debe ser igual a la raiz cuadrada de la suma de las magnitudes en la frecuencia

rms_val = np.sqrt(np.mean(Audiodata**2))

SumMagnitude = np.sqrt(np.sum(MagFreq))

print(f'RMS (tiempo) = {rms_val} y la suma de los picos de Magnitud (Frec) = {SumMagnitude}')
print('Los valores son iguales \U0001f603');

RMS (tiempo) = 0.5460872783841473 y la suma de los picos de Magnitud (Frec) = 0.5460872783841474
Los valores son iguales 😃

Espectrograma

Matplotlib (https://matplotlib.org/api/_as_gen/matplotlib.pyplot.specgram.html)
Scipy (https://docs.scipy.org/doc/scipy/reference/generated/scipy.signal.spectrogram.html)
Librosa ()

Matplotlib

Fs, data = wavfile.read(AudioName)
data = data/(2.**15) # Escalar la señal entre [-1, 1] para un audio de 16 bits
N = 512 #Numero de puntos de la fft
from scipy import signal
Pxx, freqs, bins, im = plt.specgram(data, NFFT=N, Fs=Fs,window = signal.blackman(N),noverlap = 128)
plt.title('Espectrograma con Matplotlib',size=16);
plt.ylabel('Frecuencia [Hz]'); plt.xlabel('Tiempo [Seg]');

Plotly (Interactivo) 3D

# importar la libreria plotly offline para graficar
import plotly.offline as pyo # realizar graficas offline
from plotly.offline import init_notebook_mode #para poder graficar dentro del jupyter notebook
import plotly.graph_objs as go
init_notebook_mode() # inicializar el uso de pltly dentro del jupyter noteboo

from scipy.io import wavfile # scipy library to read wav files
AudioName = "Whistle.wav" # Audio File
fs, Audiodata = wavfile.read(AudioName)
Audiodata = Audiodata / (2.**15)


#Spectrogram
from scipy import signal
plt.figure()
N = 512 #Number of point in the fft
w = signal.blackman(N)
freqs, bins, Pxx = signal.spectrogram(Audiodata, fs,window = w,nfft=N)

# Plot with plotly
trace = [go.Surface(x= bins,y= freqs,z=10*np.log10(Pxx))]

layout = go.Layout(
    title = 'Espectrograma con plotly',
    yaxis = dict(title = 'Frecuencia'), # x-axis label
    xaxis = dict(title = 'Tiempo'), # y-axis label
 );

fig = go.Figure(data=trace, layout=layout)
pyo.iplot(fig, filename='Spectrogram');

Plotly (Interactivo) Heatmap

trace = [go.Heatmap(
    x= bins,
    y= freqs,
    z= Pxx,
    colorscale='Jet',
    )]
layout = go.Layout(
    title = 'Espectrograma',
    yaxis = dict(title = 'Frequency'), # x-axis label
    xaxis = dict(title = 'Time'), # y-axis label

)
fig = go.Figure(data=trace, layout=layout)

pyo.iplot(fig, filename='Espectrograma')

Scipy

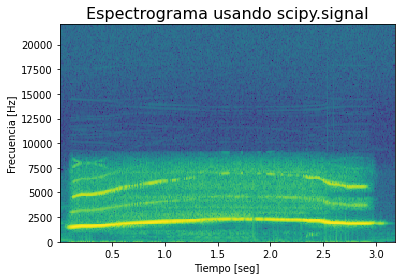
#Espectro usando scipy
Fs, data = wavfile.read(AudioName)
data = data/(2.**15) # Escalar la señal entre [-1, 1] para un audio de 16 bits
N = 512 #Numero de puntos de la fft
from scipy import signal
f, t, Sxx = signal.spectrogram(data, Fs,window = signal.blackman(N),nfft=N)
plt.pcolormesh(t, f,10*np.log10(Sxx)) # Espectro de magnitud en dB
#plt.pcolormesh(t, f,Sxx) #Espectro de Magnitud Lineal
plt.ylabel('Frecuencia [Hz]')
plt.xlabel('Tiempo [seg]')
plt.title('Espectrograma usando scipy.signal',size=16);

Librosa

X = librosa.stft(x)
Xdb = librosa.amplitude_to_db(abs(X)) # convertir la amplitud a dB
plt.figure(figsize=(14, 5))
librosa.display.specshow(Xdb, sr=sr, x_axis='time', y_axis='hz');

Aliasing

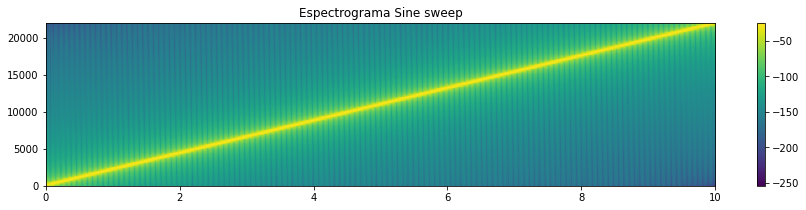
from scipy.signal import chirp
fs = 44100 # frecuencia de muestreo
T = 10 # Duracion en segundos
t = np.linspace(0, T, T*fs, endpoint=False)
# crear un sonido que va subiendo en frecuencia 20 Hz a 22050 Hz
w = np.float32(chirp(t, f0=20, f1=22050, t1=T, method='linear'))
wavfile.write('sine_sweep_44100.wav',fs,w)

plt.figure(figsize=(15,3))
plt.specgram(w, Fs=44100); plt.colorbar(); plt.title('Espectrograma Sine sweep')
_=plt.axis((0,10,0,22050))
ipd.Audio('sine_sweep_44100.wav')

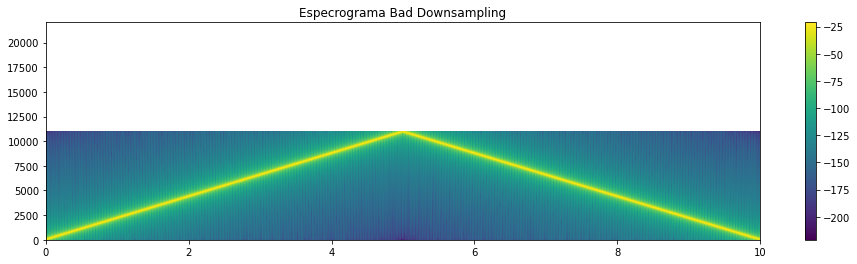
down_sampled = w[::2] # tomar datos con un brinco de 2
wavfile.write('sine_sweep_downsampled.wav',22050, down_sampled)
plt.figure(figsize=(16,4))
plt.specgram(down_sampled, Fs=22050); plt.colorbar();plt.title('Especrograma Bad Downsampling')
_=plt.axis((0,10,0,22050))
ipd.Audio('sine_sweep_downsampled.wav')

Timbre

Timbre es la cualidad del sonido que distingue el tono de diferentes instrumentos y voces, incluso si los sonidos tienen el mismo tono y volumen.

Variaciones en el Tiempo

Una característica del timbre es su evolución temporal. La envolvente de una señal es una curva suave que se aproxima a los extremos de amplitud de una forma de onda a lo largo del tiempo.

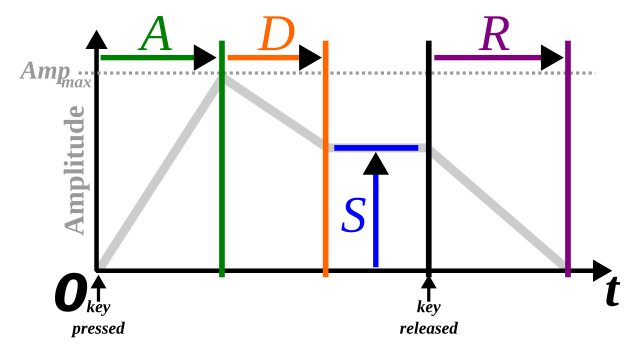
Cuando se produce un sonido su volumen y el contenido espectral cambia a través del tiempo. El “attack” (ataque) y “decay” (decaimiento) tienen un gran efecto sobre las cualidades del sonido la llamada envolvente ADSR (Attack Decay Sustain Release). El comportamiento de una envolvente de ADSR está especificado a través de cuatro parámetros:

Attack time (tiempo de ataque): es el tiempo que le toma ir de un valor inicial a un valor pico.
Decay time (tiempo de decaimiento): es el tiempo, posterior al ataque, que le toma llegar a un nivel determinado de sustain.
Sustain level (tiempo de sostenimiento): es el nivel que mantiene la secuencia del sonido durante el tiempo que dure el mismo.
Release time (tiempo de liberación): es el tiempo que le toma decaer al sonido, después del sustain, a un nivel igual a cero.

La envolvente ADSR es una simplificacion y no necesariamente modela todos los sonidos

Variaciones en la frecuencia

Otra propiedad utilizada para caracterizar el timbre es la existencia de parciales y sus Amplitudes relativas. Los parciales son las frecuencias dominantes en un tono, siendo el parcial más bajo la frecuencia fundamental.

Los parciales de un sonido se visualizan con un espectrograma. Un espectrograma muestra la intensidad de los componentes de frecuencia a lo largo del tiempo.

Tono Puro

Vamos a crear un tono artificial a 1047 HZ, equivalente a un DO en la sexta octava (C6)

T = 2.0 # segundos
f0 = 1047.0 #Frecuencia del tono
sr = 22050 # Frecuencia de Muestreo
t = np.linspace(0, T, int(T*sr), endpoint=False) # creacion del eje de tiempo
x = 0.1*np.sin(2*np.pi*f0*t) # Señal Sinusoidal
ipd.Audio(x, rate=sr)

Espectro del tono puro

X = fft(x[:4096])
X1_mag = np.absolute(X)        # Espectro de magnitud
f = np.linspace(0, sr, 4096)  # frequency variable
px.line(x = f[:2000], y= 10*np.log10(X1_mag[:2000]), labels={'x':'Frecuencia [Hz]'})

Oboe

Sonido de un oboe tocando un C6:

sr,x = wavfile.read('oboe_c6.wav')
ipd.Audio(x, rate=sr)

x=x/(2**15) # Normalizar el audio entre 1 y -1
print(x.shape)

(23625,)

Espectro del oboe:

X = fft(x[10000:14096])
X2_mag = np.absolute(X)
px.line(x =f[:2000], y= 10*np.log10(X2_mag[:2000]), labels={'x':'Frecuencia [Hz]'}) # Espectro de magnitud

Clarinete

Clarinete tocando un C6

x, sr = librosa.load('clarinet_c6.wav')
ipd.Audio(x, rate=sr)

print(x.shape)

(51386,)

X = fft(x[10000:14096])
X3_mag = np.absolute(X)
px.line(x =f[:2000], y= 10*np.log10(X3_mag[:2000]), labels={'x':'Frecuencia [Hz]'}) # Espectro de magnitud

# Grafica con Matplotlib
#plt.plot(f[:2000], 10*np.log10(X1_mag[:2000]),'r',label = 'Sinusoidal') # magnitude spectrum
#plt.plot(f[:2000], 10*np.log10(X2_mag[:2000]),'b',label = 'Oboe') # magnitude spectrum
#plt.plot(f[:2000], 10*np.log10(X3_mag[:2000]),'g',label = 'Clarinete') # magnitude spectrum
#plt.title('Espectro de Sinusoide, Oboe y Clarinete en la misma nota');plt.legend();

#Grafica con Plotly
from itertools import cycle

fig = px.line(x = f[:2000],
        y= [10*np.log10(X1_mag[:2000]), 10*np.log10(X2_mag[:2000]), 10*np.log10(X3_mag[:2000])],
        title = 'Espectro de Sinusoide, Oboe y Clarinete en la misma nota'
        )
names = cycle(['Sinusoidal', 'Oboe', 'Clarinete'])
fig.for_each_trace(lambda t:  t.update(name = next(names)))
fig.show()

Observe la diferencia en las amplitudes relativas de los componentes parciales. Las tres señales tienen aproximadamente el mismo tono y frecuencia fundamental, sin embargo, sus timbres son diferentes.

Representacion del Audio