Por Jose R. Zapata
import numpy as np
import IPython.display as ipd
import librosa, librosa.display
import matplotlib.pyplot as plt
Escala de Magnitud
A menudo, la amplitud original de una señal en el dominio de tiempo o de lafrecuencia no es perceptualmente relevante para los humanos como la amplitud convertida en otras unidades, Ej: usar una escala logarítmica.
Por ejemplo, consideremos un tono puro cuya amplitud aumenta de forma lineal. Definir la variable de tiempo:
T = 5.0 # duracion en segundos
sr = 22050 # Frecuencia de muestreo en Hz
t = np.linspace(0, T, int(T*sr), endpoint=False)
Crear una señal que su amplitud aumente linealmente
amplitude = np.linspace(0, 1, int(T*sr), endpoint=False) # Amplitud variable en el tiempo
x = amplitude*np.sin(2*np.pi*440*t) #Señal sinusoidal
ipd.Audio(x, rate=sr)
Grafica de la señal:
librosa.display.waveplot(x, sr=sr);

Ahora considere una señal cuya amplitud crece exponencialmente, es decir, el logaritmo de la amplitud es lineal:
amplitude = np.logspace(-2, 0, int(T*sr), endpoint=False, base=10.0)
x = amplitude*np.sin(2*np.pi*440*t)
ipd.Audio(x, rate=sr)
librosa.display.waveplot(x, sr=sr);

A pesar de que la amplitud crece exponencialmente, para nosotros, el aumento en el volumen parece más gradual. Este fenómeno es un ejemplo de la ley Weber-Fechner law (Wikipedia)que establece que la relación entre un estímulo y la percepción humana es logarítmica.
Percepcion de la amplitud segun la frecuencia
T = 4.0 # duracion en segundos
sr = 44100 # Frecuencia de muestreo en Hz
t = np.linspace(0, T, int(T*sr), endpoint=False)
100 Hz
# 100 Hz
x1 = np.sin(2*np.pi*100*t)
ipd.Audio(x1, rate=sr)
250 Hz
#250 hz
x2 = np.sin(2*np.pi*250*t)
ipd.Audio(x2, rate=sr)
400 Hz
#400 hz
x3 = np.sin(2*np.pi*400*t)
ipd.Audio(x3, rate=sr)
1000 Hz
#1000 hz
x4 = np.sin(2*np.pi*1000*t)
ipd.Audio(x4, rate=sr)
4000 Hz
#4000 hz
x5 = np.sin(2*np.pi*4000*t)
ipd.Audio(x5, rate=sr)
10000 Hz
#10000 hz
x6 = np.sin(2*np.pi*10000*t)
ipd.Audio(x6, rate=sr)
15000 Hz
#15000 hz
x7 = np.sin(2*np.pi*15000*t)
ipd.Audio(x7, rate=sr)
18000 Hz
#18000 hz
x8 = np.sin(2*np.pi*18000*t)
ipd.Audio(x8, rate=sr)
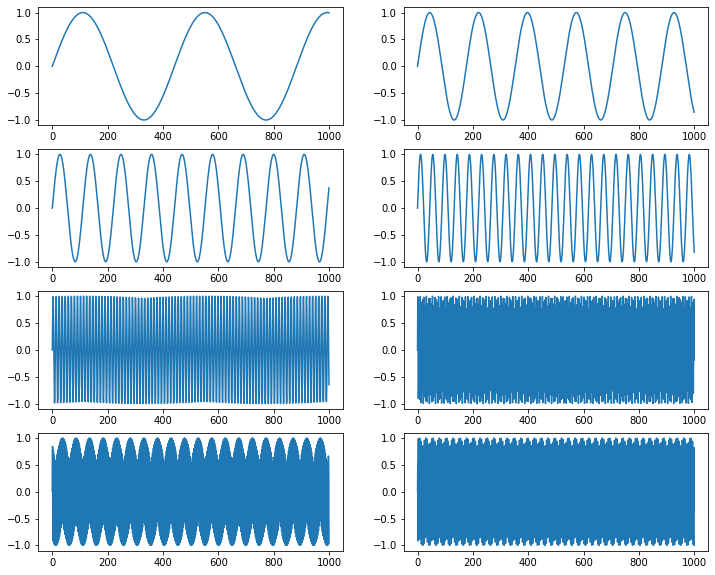
Graficas de las señales
plt.figure(figsize=(12,10))
for n in range(8):
plt.subplot(4,2,n+1)
plt.plot(eval('x'+str(n+1))[:1000])# graficar los primeros 1000 valores
Enmascaramiento Simultaneo
400 Hz
# Audio de 400 Hz
x1, sr1 = librosa.load('./Data/400Hz.wav',sr=None)
X1 = librosa.stft(x1)
Xdb1 = librosa.amplitude_to_db(abs(X1)) # convertir la amplitud a dB
plt.figure(figsize=(14, 5))
librosa.display.specshow(Xdb1, sr=sr1, x_axis='time', y_axis='hz');
ipd.Audio(x1,rate=sr1)

500 Hz
x2, sr2 = librosa.load('./Data/500Hz.wav',sr=None)
X2 = librosa.stft(x2)
Xdb2 = librosa.amplitude_to_db(abs(X2)) # convertir la amplitud a dB
plt.figure(figsize=(14, 5))
librosa.display.specshow(Xdb2, sr=sr2, x_axis='time', y_axis='hz');
ipd.Audio(x2,rate=sr2)

400 Hz + 500 Hz
x3, sr3 = librosa.load('./Data/400Hz+500Hz.wav',sr=None)
X3 = librosa.stft(x3)
Xdb3 = librosa.amplitude_to_db(abs(X3)) # convertir la amplitud a dB
plt.figure(figsize=(14, 5))
librosa.display.specshow(Xdb3, sr=sr3, x_axis='time', y_axis='hz');
ipd.Audio(x3,rate=sr3)
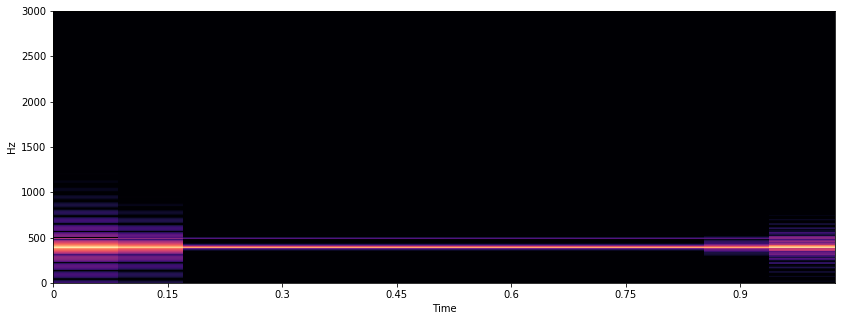
Audios finales
ipd.display(ipd.Audio(x1,rate=sr1)) #400 Hz
ipd.display(ipd.Audio(x2,rate=sr2)) #500 Hz
ipd.display(ipd.Audio(x3,rate=sr3)) #400 Hz + 500 Hz
Phd. Jose R. Zapata
