Extraccion de Caracteristicas (Ejemplo)
Debemos extraer las características de nuestra señal de audio que son más relevantes para el problema que estamos tratando de resolver. Por ejemplo, si queremos clasificar algunos sonidos por el timbre, buscaremos características que distingan los sonidos por su timbre y no por su tono. Si queremos realizar la detección de tono, queremos características que distingan el tono y no el timbre.
Este proceso se conoce como extracción de características (feature extraction).
Vamos a hacer un ejemplo con veinte archivos de audio: diez muestras de bombo (Kick Drum) y diez muestras de redoblante de batería (snare drum). Cada archivo de audio contiene un golpe de batería.
# Importar librerias
from pathlib import Path
from scipy.io import wavfile
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt, IPython.display as ipd
import librosa, librosa.display
# leer los archivos y guardarlos
kick_signals = [
librosa.load(p)[0] for p in Path().glob('Data/drum_samples/train/kick_*.mp3')
]
snare_signals = [
librosa.load(p)[0] for p in Path().glob('Data/drum_samples/train/snare_*.mp3')
]
kick_signals[0].dtype
dtype('float32')
# Escuchar un ejemplo de los kick drums
ipd.Audio('Data/drum_samples/train/kick_08.mp3')
len(kick_signals)
# escuchar uno de los audios de kick drums
10
# Escuchar un Ejemplo de los snare drums
ipd.Audio('Data/drum_samples/train/snare_08.mp3')
len(snare_signals)
10
Graficar los audios de los kick drums:
plt.figure(figsize=(15, 6))
for i, x in enumerate(kick_signals):
plt.subplot(2, 5, i+1)
librosa.display.waveplot(x[:10000])
plt.ylim(-1, 1)
plt.tight_layout()
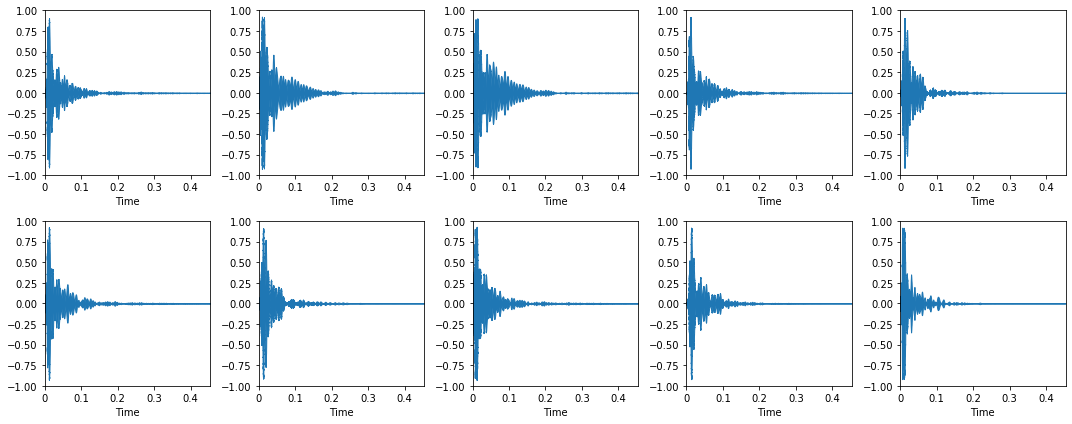
Graficar los audios de los snare drum:
plt.figure(figsize=(15, 6))
for i, x in enumerate(snare_signals):
plt.subplot(2, 5, i+1)
librosa.display.waveplot(x[:10000])
plt.ylim(-1, 1)
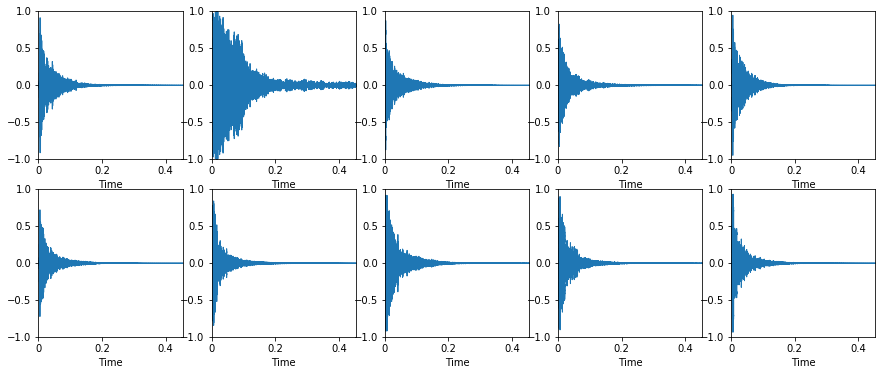
Construir el vector de caracteristicas (Feature Vector)
Un feature vector es simplemente una colección de características. Aquí hay una función simple que construye un vector de característica bidimensional a partir de una señal, calculando el numero de cruces por cero de la señal y el centroide del espectro:
def extract_features(signal):
return [
librosa.feature.zero_crossing_rate(signal)[0, 0], #Numero de cruces por cero
librosa.feature.spectral_centroid(signal)[0, 0], # centroide del espectro
]
Si queremos agregar todos los vectores de características entre las señales de una colección, podemos usar una list comprehension de la siguiente manera:
kick_features = np.array([extract_features(x) for x in kick_signals])
snare_features = np.array([extract_features(x) for x in snare_signals])
kick_features
array([[1.56250000e-02, 1.06834727e+03],
[1.46484375e-02, 1.54304375e+03],
[1.66015625e-02, 2.02466876e+03],
[1.31835938e-02, 1.01799629e+03],
[1.17187500e-02, 9.96149687e+02],
[1.75781250e-02, 1.07787287e+03],
[1.46484375e-02, 1.23806608e+03],
[2.00195312e-02, 1.95042545e+03],
[1.51367188e-02, 9.42650772e+02],
[9.27734375e-03, 5.91587139e+02]])
snare_features
array([[9.13085938e-02, 2.55004881e+03],
[1.03027344e-01, 2.83001990e+03],
[9.32617188e-02, 2.64940354e+03],
[7.86132812e-02, 2.67948194e+03],
[8.49609375e-02, 2.79784112e+03],
[7.22656250e-02, 2.10371277e+03],
[7.71484375e-02, 2.59464452e+03],
[6.54296875e-02, 2.56543930e+03],
[7.03125000e-02, 2.62956924e+03],
[6.88476562e-02, 2.27723009e+03]])
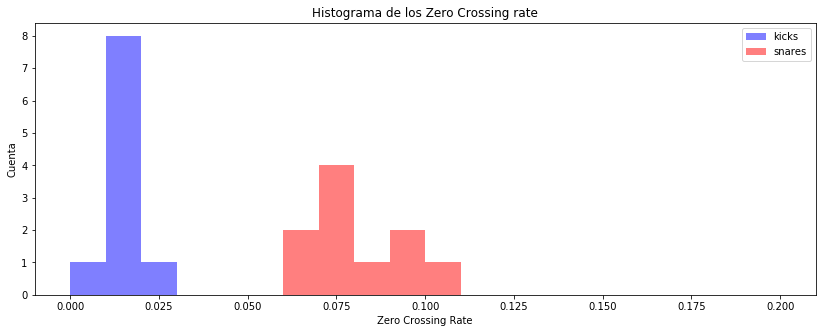
Visualice las diferencias en las características al trazar histogramas separados para cada una de las clases:
plt.figure(figsize=(14, 5))
plt.hist(kick_features[:,0], color='b', range=(0, 0.2), alpha=0.5, bins=20)
plt.hist(snare_features[:,0], color='r', range=(0, 0.2), alpha=0.5, bins=20)
plt.legend(('kicks', 'snares'))
plt.title('Histograma de los Zero Crossing rate')
plt.xlabel('Zero Crossing Rate')
plt.ylabel('Cuenta');
plt.figure(figsize=(14, 5))
plt.hist(kick_features[:,1], color='b', range=(0, 4000), bins=30, alpha=0.6)
plt.hist(snare_features[:,1], color='r', range=(0, 4000), bins=30, alpha=0.6)
plt.legend(('kicks', 'snares'))
plt.title('Histograma de los spectral centroid')
plt.xlabel('Spectral Centroid (frequency bin)')
plt.ylabel('Cuenta');
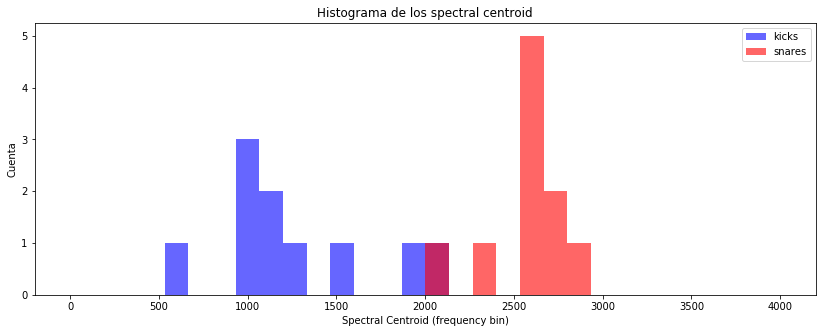
Escalamiento de las caracteristicas (Feature Scaling)
Las características que usamos en el ejemplo anterior incluyen el zero crossing rate (tasa de cruce por cero) y el spectral centroid (centroide espectral). Estas dos características se expresan usando diferentes unidades. Esta discrepancia puede plantear problemas al realizar la clasificación más tarde. Por lo tanto, normalizaremos cada vector de características a un rango común y almacenaremos los parámetros de normalización para un uso posterior.
Existen muchas técnicas para escalar tus características. Usaremos sklearn.preprocessing.MinMaxScaler. MinMaxScaler devuelve una matriz de valores escalados de modo que cada dimensión está en el rango de -1 a 1.
Vamos a concatenar todos nuestros vectores de características en una tabla de características:
feature_table = np.vstack((kick_features, snare_features))
print(feature_table.shape)
(20, 2)
La escala de cada caracteeristica estara en el rango de -1 to 1:
import sklearn
scaler = sklearn.preprocessing.MinMaxScaler(feature_range=(-1, 1))
training_features = scaler.fit_transform(feature_table)
print(training_features.min(axis=0))
print(training_features.max(axis=0))
[-1. -1.]
[1. 1.]
Graficar las caracteristicas escaladas:
plt.figure(figsize=(14, 5))
plt.scatter(training_features[:10,0], training_features[:10,1], c='b')
plt.scatter(training_features[10:,0], training_features[10:,1], c='r')
plt.legend(('kicks', 'snares'))
plt.title('Zero Crossing rate Vs Spectral centroid')
plt.xlabel('Zero Crossing Rate')
plt.ylabel('Spectral Centroid');

Segmentacion
En el procesamiento de audio, es común operar en un segmento a la vez usando un tamaño constante y longitud de salto (incremento) constante. Los segmentos generalmente se eligen para que esten entre 10 y 100 ms de duración.
Vamos a crear una señal de audio que consiste en un tono puro que gradualmente se hace más fuerte. Luego, segmentaremos la señal y calcularemos la energía cuadrática media (RMS), root mean square (RMS) energy para cada segmento.
Primero, establecer nuestros parámetros:
T = 3.0 # duracion en segundos
sr = 22050 # frecuencia de muestreo en Hertz
# La amplitud ser a creciente logaritmicamente
amplitude = np.logspace(-3, 0, int(T*sr), endpoint=False, base=10.0) # amplitud variable en el tiempo
print(amplitude.min(), amplitude.max()) # empieza en 110 Hz, termina en 880 Hz
0.001 0.9998955798243658
Crear la señal:
t = np.linspace(0, T, int(T*sr), endpoint=False)
x = amplitude*np.sin(2*np.pi*440*t)
# Escuchar la señal
ipd.Audio(x, rate=sr)
Graficar la señal:
plt.figure(figsize=(14, 5))
librosa.display.waveplot(x, sr=sr);
Segmentacion usando List Comprehensions de Python
Podemos usar el list comprehension para realizar la segmentacion y calcular el RMSE al mismo tiempo.
# Inicializar los parametros
frame_length = 1024 #tamaño de muestras de los segmentos
hop_length = 512 # tamaño del incremento, en este caso es la mitad del valor del segmento
Definir la funcion para calcular el RMSE:
def rmse(x):
return np.sqrt(np.mean(x**2))
Usar la list comprehension, luego graficar el RMSE de cada segmento en un eje log-y:
plt.figure(figsize=(14, 5))
plt.semilogy([rmse(x[i:i+frame_length])
for i in range(0, len(x), hop_length)]);
plt.title('Energia Creciente Logaritmicamente');

funcion librosa.util.frame
Dada una señal, librosa.util.frame produce una lista de segmentos de tamaño uniforme:
plt.figure(figsize=(14, 5))
frames = librosa.util.frame(x, frame_length=frame_length, hop_length=hop_length)
plt.semilogy([rmse(frame) for frame in frames.T]);
plt.title('Energia Creciente Logaritmicamente');

Normalmente los metodos de extracion de caracteristicas (feature extraction) realizan la segmentacion automaticamente.
Energia y RMSE
La Energia de una señal corresponde a suma total de las magnitudes de la señal. Para señales de Audio, aproximadamente corresponde a qué tan fuerte es la señal en terminos de volumen. La energía en una señal se define como:
$$\sum_n \left| x(n) \right|^2$$
El root-mean-square energy (RMSE) en una señal se define como:
$$\sqrt{ \frac{1}{N} \sum_n \left| x(n) \right|^2 }$$
#Cargar una señal
x, sr = librosa.load('Data/simple_loop.wav')
sr # frecuencia de muestreo
22050
x.shape # Tamaño
(49613,)
librosa.get_duration(x, sr) # duracion
2.2500226757369615
ipd.Audio(x, rate=sr)
# Graficar la señal
librosa.display.waveplot(x, sr=sr);
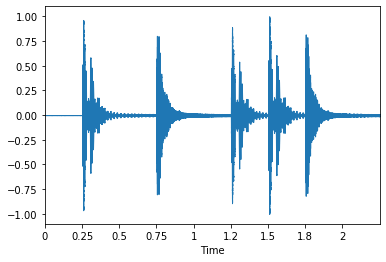
#Calcular el la energia por segmentos pequeños (short-time) usando list comprehension:
hop_length = 256 # tamaño del incremento
frame_length = 512 # tamaño del segmento
energy = np.array([
sum(abs(x[i:i+frame_length]**2))
for i in range(0, len(x), hop_length)
])
energy.shape
(194,)
Calcular el RMSE usando librosa.feature.rmse:
rmse = librosa.feature.rms(x, frame_length=frame_length, hop_length=hop_length, center=True)
rmse.shape
(1, 194)
rmse = rmse[0]
Graficar la energia y el RMSE juntas con la forma de onda:
frames = range(len(energy))
t = librosa.frames_to_time(frames, sr=sr, hop_length=hop_length)
plt.figure(figsize=(14, 5))
librosa.display.waveplot(x, sr=sr, alpha=0.4)
plt.plot(t, energy/energy.max(), 'r--') # normalizada para la visualizacion
plt.plot(t[:len(rmse)], rmse/rmse.max(), color='g') # normalizada para la visualizacion
plt.legend(('Energia', 'RMSE'));
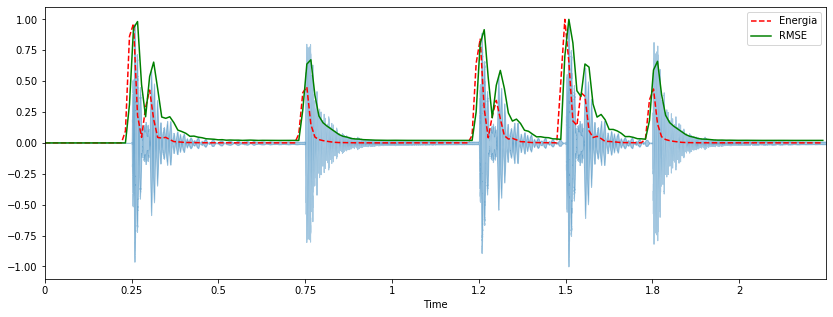
Zero Crossing Rate (Numero de cruces por cero)
El zero crossing rate indica el numero de veces que la señal cruza el eje horizontal por cero.
# Cargar la señal de audio
x, sr = librosa.load('Data/simple_loop.wav')
ipd.Audio(x, rate=sr)
# graficar la señal
plt.figure(figsize=(14, 5))
librosa.display.waveplot(x, sr=sr);
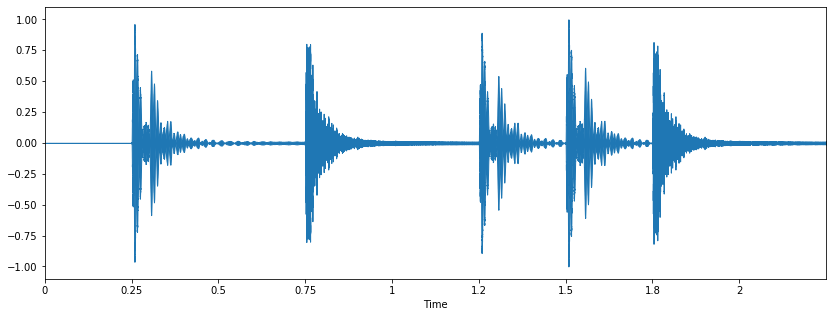
Hacer un zoom:
n0 = 6500
n1 = 7500
plt.figure(figsize=(14, 5))
plt.plot(x[n0:n1]);
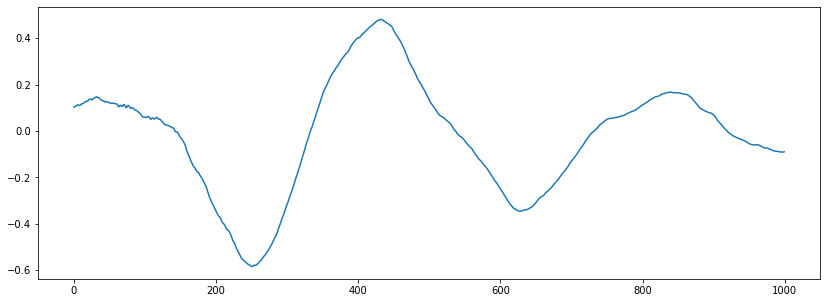
Se pueden contan 5 cruces por cero. Vamos a realizar el calculo del zero crossings usando librosa.
zero_crossings = librosa.zero_crossings(x[n0:n1], pad=False)
zero_crossings.shape
(1000,)
Este calculo nos da un valor True indicando que hubo un cruce por cero. Para caluclar el zero crossings se debe sumar sum:
print(sum(zero_crossings))
5
Para calcular el zero-crossing rate en el tiempo se usazero_crossing_rate:
zcrs = librosa.feature.zero_crossing_rate(x)
print(zcrs.shape)
(1, 97)
Graficar el zero-crossing rate:
plt.figure(figsize=(14, 5))
plt.plot(zcrs[0]);
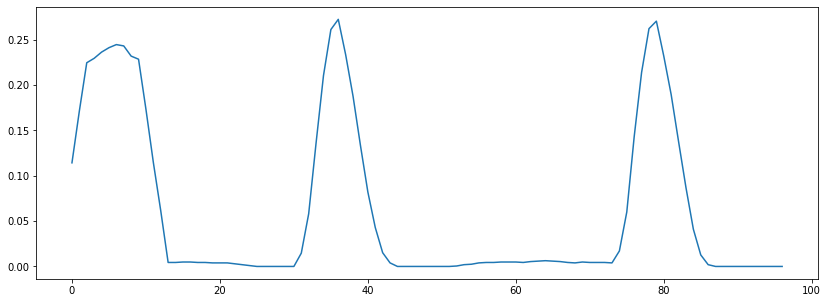
Observe que el valor del zero-crossing rate aumenta cuando hay un snare drum.
La razon por la que hay un valor grande al inicio es por que en el ‘silencio’ hay una oscilacion del ruido cerca del cero.
plt.figure(figsize=(14, 5))
plt.plot(x[:1000])
plt.ylim(-0.0001, 0.0001);
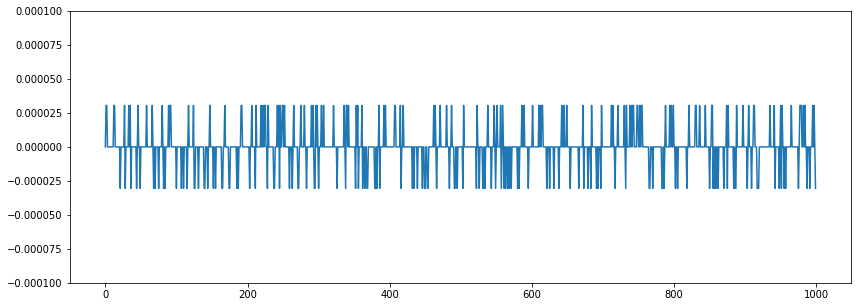
Un simple truco es sumar una pequeña constante antes de calcular el zero crossing rate:
zcrs = librosa.feature.zero_crossing_rate(x + 0.0001)# señal mas una cantidad pequeña
plt.figure(figsize=(14, 5))
plt.plot(zcrs[0]);
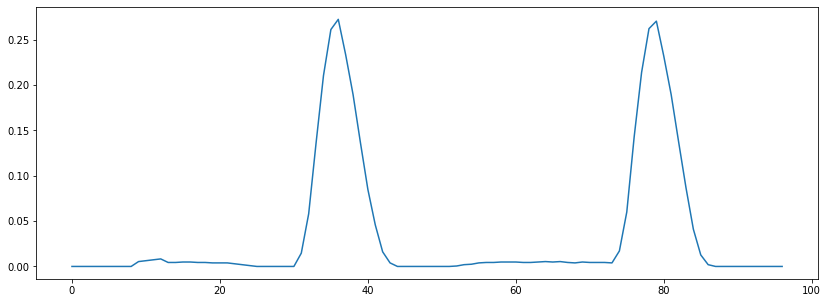
STFT - Transformada corta de Fourier (Short-Time Fourier Transform)
Las señales de audio no estacionarias, es decir, sus estadísticas cambian con el tiempo. No tendría sentido calcular una sola transformada de Fourier en un audio completo de 10 minutos.
La short-time Fourier transform (STFT) (Wikipedia se obtiene calculando la transformada de Fourier para segmentos sucesivos en una señal.
$$ X(m, \omega) = \sum_n x(n) w(n-m) e^{-j \omega n} $$
A medida que aumentamos $m$, deslizamos la función de ventana $w$ hacia la derecha. Para el segmento resultante, $x(n)w(n-m)$, calculamos la transformada de Fourier. Por lo tanto, STFT $X$ es una función de tiempo, $m$ y frecuencia, $\omega$.
librosa.stft realiza el calculo de la STFT.
Se debe especificar el tamaño del segmento (frame size) y el incremento (hop size).
x, sr = librosa.load('Data/Journey.wav')
ipd.Audio(x, rate=sr)
hop_length = 512 #incremento
n_fft = 2048 #Tamaño del segmento
X = librosa.stft(x, n_fft=n_fft, hop_length=hop_length)
Para convertir el tamaño del segmento y el incremento en segundos:
float(hop_length)/sr # [=] segundos
0.023219954648526078
float(n_fft)/sr # [=] segundos
0.09287981859410431
Para las señales de valor real, la transformada de Fourier es simétrica con respecto al punto medio.
Entonces, librosa.stft solo conserva la mitad de los valores calculados.
X.shape
(1025, 686)
Esta STFT tiene 1025 bins de frecuencia y 686 de segmentos en el tiempo.
Espectrograma
En el procesamiento de Audio, a menudo solo importa el especrto de magnitud y no el contenido de la fase.
El Espectrograma Wikipedia muestra la intensidad de las frecuencias a lo largo del tiempo. Un espectrograma es simplemente la magnitud al cuadrado de la STFT (Short-time Fourier Transform):
$$S(m, \omega) = \left| X(m, \omega) \right|^2$$
La percepción humana de la intensidad del sonido es de naturaleza logarítmica. Por lo tanto, a menudo nos interesa la amplitud en esacala logaritmica (db):
S = librosa.amplitude_to_db(abs(X))
Para graficar el espectrograma con librosa, se usalibrosa.display.specshow.
plt.figure(figsize=(15, 5))
librosa.display.specshow(S, sr=sr, x_axis='time', y_axis='linear');
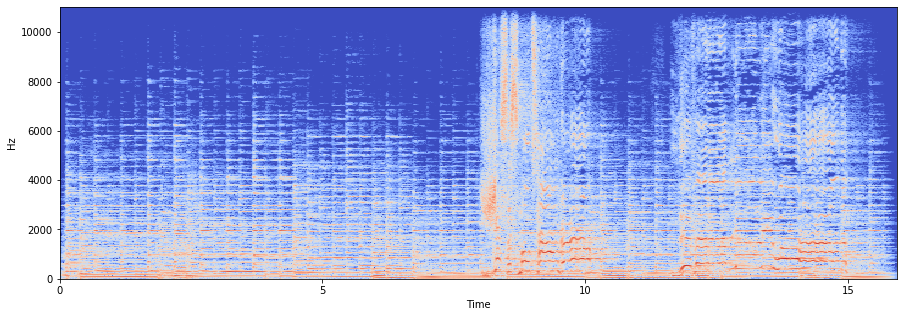
Mel-Espectrograma
librosa tiene implementada la representacion espectral, librosa.feature.melspectrogram,
La escala Mel relaciona la frecuencia percibida, o tono, de un tono puro con su frecuencia medida real. Los humanos son mucho mejores para discernir pequeños cambios en el tono a bajas frecuencias que en frecuencias altas. La incorporación de esta escala hace que nuestras características coincidan más de cerca con lo que escuchan los humanos.
S = librosa.feature.melspectrogram(x, sr=sr, n_fft=4096, hop_length=256)
La percepción humana de la intensidad del sonido es de naturaleza logarítmica. Por lo tanto, a menudo nos interesa la amplitud logaritmica:
logS = librosa.amplitude_to_db(S)
Para graficar cualquier espectrograma en librosa se usa librosa.display.specshow.
plt.figure(figsize=(15, 5))
librosa.display.specshow(logS, sr=sr, x_axis='time', y_axis='mel');
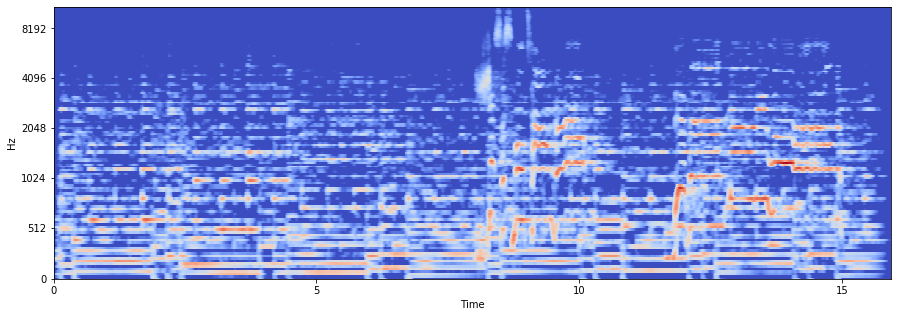
Usando y_axis=mel grafica el y-axis en la escala mel la cual es similar a la funcion $\log (1 + f)$ :
$$ m = 2595 \log_{10} \left(1 + \frac{f}{700} \right) $$ $$ m = 1127 \ln \left(1 + \frac{f}{700} \right) $$
librosa.cqt
A diferencia de la transformada de Fourier, pero similar a la escala mel, la constant-Q transform utiliza un eje de frecuencia espaciado logaritmicamente.
Para graficar el constant-Q spectrogram, podems usar librosa.cqt:
fmin = librosa.midi_to_hz(36)
C = librosa.cqt(x, sr=sr, fmin=fmin, n_bins=72)
logC = librosa.amplitude_to_db(abs(C))
plt.figure(figsize=(15, 5))
librosa.display.specshow(logC, sr=sr, x_axis='time', y_axis='cqt_note', fmin=fmin, cmap='coolwarm');
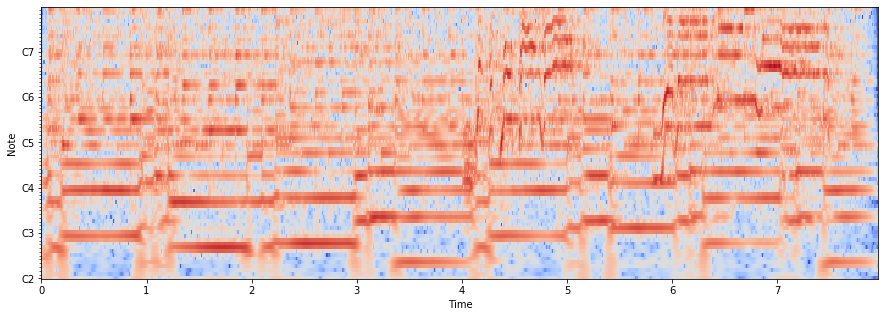
Mel Frequency Cepstral Coefficients (MFCCs)
Los Coeficientes Cepstrales en las Frecuencias de Mel o MFCCs son coeficientes para la representación del habla basados en la percepción auditiva humana y fueron presentados por Davis and Mermelstein en los 80’s. Estos surgen de la necesidad, en el área del reconocimiento de audio automático, de extraer características de las componentes de una señal de audio que sean adecuadas para la identificación de contenido relevante, así como obviar todas aquellas que posean información poco valiosa como el ruido de fondo, emociones, volumen, tono, etc. y que no aportan nada al proceso de reconocimiento, al contrario lo empobrecen. (MFCC) de una señal son un pequeño conjunto de características (por lo general, alrededor de 10-20) que describen de forma concisa la forma general de una envolvente espectral. A menudo se usa para describir el timbre.
estos se calculan asi:
- Separar la señal en pequeños segmentos.
- A cada segmento aplicarle la Transformada de Fourier discreta y obtener la potencia espectral de la señal.
- Aplicar el banco de filtros correspondientes a la Escala Mel al espectro obtenido en el paso anterior y sumar las energías en cada uno de ellos.
- Tomar el logaritmo de todas las energías de cada frecuencia mel
- Aplicarle la transformada de coseno discreta (DCT) a estos logaritmos.
- Quedarse con los coefficientes 2 al 13 de la DCT y eliminar el resto
# Graficar la onda
x, fs = librosa.load('Data/simple_loop.wav')
librosa.display.waveplot(x, sr=fs)
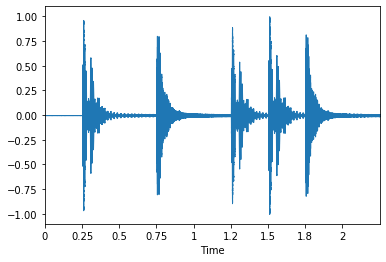
#Escuchar el sonido
ipd.Audio(x, rate=fs)
librosa.feature.mfcc
Calcular los MFCCs sobre toda la señal de audio librosa.feature.mfcc
mfccs = librosa.feature.mfcc(x, sr=fs)
mfccs.shape
(20, 97)
En este caso, se calculan 20 mfcc sobre 130 segmentos(frames).
El primer MFCC, el coeficiente 0, no transmite información relevante para la forma general del espectro. Solo transmite un desplazamiento constante, es decir, agrega un valor constante a todo el espectro. Por lo tanto, muchas personas descartan el primer MFCC cuando realizan clasificación. Por ahora, usaremos los MFCC como están.
Graficar los MFCCs:
librosa.display.specshow(mfccs, sr=fs, x_axis='time');
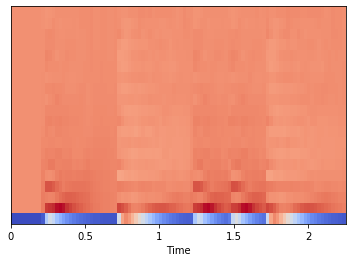
Escalamiento de Caracteristicas
Escalemos los MFCC de modo que cada dimensión de coeficiente tenga una media cero y una unidad de varianza:
mfccs = sklearn.preprocessing.scale(mfccs, axis=1)
print(mfccs.mean(axis=1))
print(mfccs.var(axis=1))
[-3.6868852e-09 1.2289617e-09 6.1448086e-10 0.0000000e+00
-2.5808196e-08 -2.1814071e-08 9.2172131e-10 8.6027319e-09
1.5208402e-08 2.0277868e-08 -2.5193716e-08 -4.6086064e-09
-1.8434426e-09 -1.2289617e-08 4.9158468e-09 -1.5362022e-09
1.9509768e-08 -1.0138934e-08 2.4579234e-09 5.8990164e-08]
[1.0000002 1.0000001 0.99999994 1.0000001 0.99999976 0.9999998
1.0000001 1.0000001 0.9999997 1. 1.0000001 1.0000001
0.99999946 1. 1. 1.0000001 0.9999998 1.0000004
1.0000001 1. ]
Graficar los MFCCs escalados:
librosa.display.specshow(mfccs, sr=fs, x_axis='time');
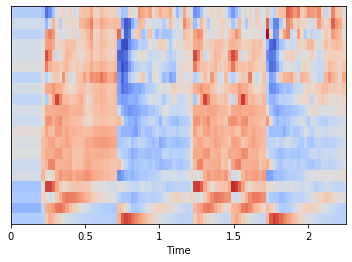
Caracteristicas Espectrales
Para clasificación de sonidos, vamos a utilizar los momentos espectrales (centroide, ancho de banda, asimetría, curtosis)(centroid, bandwidth, skewness, kurtosis) y otras estadísticas espectrales. Moments es un término usado en física y estadística. Hay momentos de centralidad y momentos de estandard.
Centroide espectral (Spectral Centroid)
# Archivo de audio
x, sr = librosa.load('Data/simple_loop.wav')
ipd.Audio(x, rate=sr)
El spectral centroid (Wikipedia) indica a qué frecuencia se centra la energía de un espectro. Esto es como una media ponderada:
$$ f_c = \frac{\sum_k S(k) f(k)}{\sum_k S(k)} $$
donde $S(k)$ es el espectro de magnitud al bin de frecuencia $k$, $f(k)$ es la frecuencia en el bin $k$.
librosa.feature.spectral_centroid calcula el spectral centroid para cada segmento en una señal:
spectral_centroids = librosa.feature.spectral_centroid(x, sr=sr)[0]
spectral_centroids.shape
(97,)
Calcular la variable de tiempo para la visualizacion:
frames = range(len(spectral_centroids))
t = librosa.frames_to_time(frames)
Definir una funcion para normalizar la visualizacion del spectral centroid:
def normalize(x, axis=0):
return sklearn.preprocessing.minmax_scale(x, axis=axis)
Graficar el spectral centroid sobre toda la forma de onda:
librosa.display.waveplot(x, sr=sr, alpha=0.4)
plt.plot(t, normalize(spectral_centroids), color='r'); # normalizacion para proposito de visualizacion
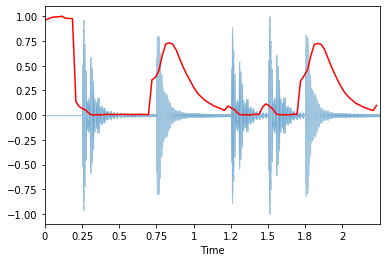
De forma similar a la tasa de cruces por cero, hay un aumento espurio en el centroide espectral al comienzo de la señal. Esto se debe a que el silencio al principio tiene una amplitud tan pequeña que los componentes de alta frecuencia tienen la oportunidad de dominar. Un truco en torno a esto es agregar una pequeña constante antes de calcular el centroide espectral, desplazando así el centroide hacia cero en las partes silenciosas:
spectral_centroids = librosa.feature.spectral_centroid(x+0.01, sr=sr)[0]
librosa.display.waveplot(x, sr=sr, alpha=0.4)
plt.plot(t, normalize(spectral_centroids), color='r'); # normalizacion para proposito de visualizacion
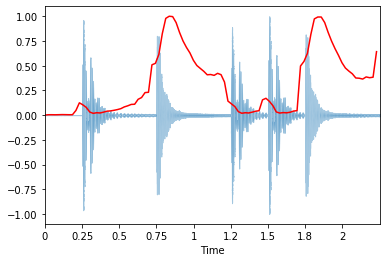
Ancho de Banda espectral (Spectral Bandwidth)
librosa.feature.spectral_bandwidth calcula el orden-$p$ del ancho de banda espectral (spectral bandwidth):
$$ \left( \sum_k S(k) \left(f(k) - f_c \right)^p \right)^{\frac{1}{p}} $$
Donda $S(k)$ es el espectro de magnitud al bin de frecuencia $k$, $f(k)$ es la frecuencia del bin $k$, y $f_c$ es ele spectral centroid. Cuando $p = 2$, es como una desviacion estandard ponderada.
spectral_bandwidth_2 = librosa.feature.spectral_bandwidth(x+0.01, sr=sr)[0]
spectral_bandwidth_3 = librosa.feature.spectral_bandwidth(x+0.01, sr=sr, p=3)[0]
spectral_bandwidth_4 = librosa.feature.spectral_bandwidth(x+0.01, sr=sr, p=4)[0]
librosa.display.waveplot(x, sr=sr, alpha=0.4)
plt.plot(t, normalize(spectral_bandwidth_2), color='r')
plt.plot(t, normalize(spectral_bandwidth_3), color='g')
plt.plot(t, normalize(spectral_bandwidth_4), color='y')
plt.legend(('p = 2', 'p = 3', 'p = 4'));
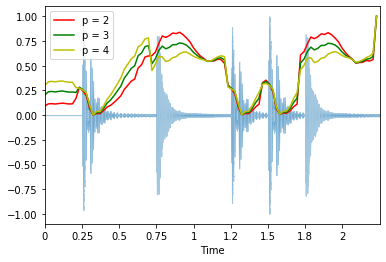
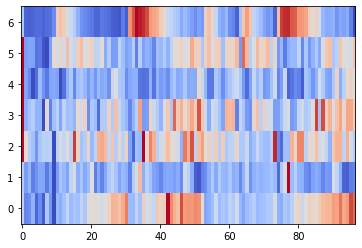
contraste Espectral (Spectral Contrast)
El Spectral contrast considera los picos espectrales, y los ‘valles’ espectrales, y sus diferencias en cada subbanda de frecuencia. Para mas informacion:
Para calcular el spectral contrast para seis subbandas para cada segmento se puede usar librosa.feature.spectral_contrast
spectral_contrast = librosa.feature.spectral_contrast(x, sr=sr)
spectral_contrast.shape
(7, 97)
Graficar:
plt.imshow(normalize(spectral_contrast, axis=1), aspect='auto', origin='lower', cmap='coolwarm');
Desplazamiento espectral (Spectral Rolloff)
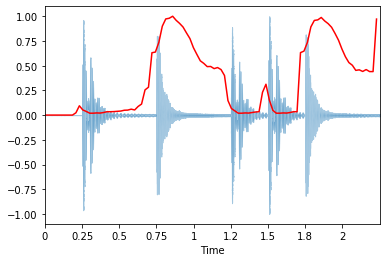
El Spectral rolloff es la frecuencia por debajo de la cual un porcentaje específico de la energía espectral total se enceuntra, normalmente el 85%
Para Calcular la frecuencia de rolloff para cada segmento en la señal podemos usar librosa.feature.spectral_rolloff
spectral_rolloff = librosa.feature.spectral_rolloff(x+0.01, sr=sr)[0]
librosa.display.waveplot(x, sr=sr, alpha=0.4)
plt.plot(t, normalize(spectral_rolloff), color='r');
Libreria pyAudioAnalysis
Con esta libreria podemos realizar la extraccion (low-term) de varias caracteristicas de una señal de audio
- Zero Crossing Rate The rate of sign-changes of the signal during the duration of a particular frame.
- Energy The sum of squares of the signal values, normalized by the respective frame length.
- Entropy of Energy The entropy of sub-frames’ normalized energies. It can be interpreted as a measure of abrupt changes.
- Spectral Centroid The center of gravity of the spectrum.
- Spectral Spread The second central moment of the spectrum.
- Spectral Entropy Entropy of the normalized spectral energies for a set of sub-frames.
- Spectral Flux The squared difference between the normalized magnitudes of the spectra of the two successive frames.
- Spectral Rolloff The frequency below which 90% of the magnitude distribution of the spectrum is concentrated.
- MFCCs Mel Frequency Cepstral Coefficients form a cepstral representation where the frequency bands are not linear but distributed according to the mel-scale.
- Chroma Vector A 12-element representation of the spectral energy where the bins represent the 12 equal-tempered pitch classes of western-type music (semitone spacing).
- Chroma Deviation The standard deviation of the 12 chroma coefficients.
#Instalacion de librerias
#!conda install -c anaconda simplejson
#!pip install eyeD3
#!pip install pydub
#!pip install pyAudioAnalysis
# Importar librerias
from pyAudioAnalysis import audioBasicIO
from pyAudioAnalysis import audioFeatureExtraction
import matplotlib.pyplot as plt
%matplotlib inline
import math
[Fs, x] = audioBasicIO.readAudioFile("./Data/Whistle.wav");
# tamaño del segmento 50 msegs y un incremento de 25 msegs (50% superposicion)
F, f_names = audioFeatureExtraction.stFeatureExtraction(x, Fs, 0.050*Fs, 0.025*Fs);
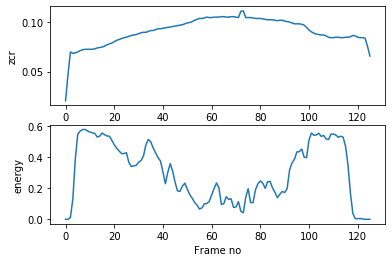
Se extraen las low-term features de la señal
plt.subplot(2,1,1); plt.plot(F[0,:]); plt.xlabel('Frame no'); plt.ylabel(f_names[0]);
plt.subplot(2,1,2); plt.plot(F[1,:]); plt.xlabel('Frame no'); plt.ylabel(f_names[1]); plt.show()
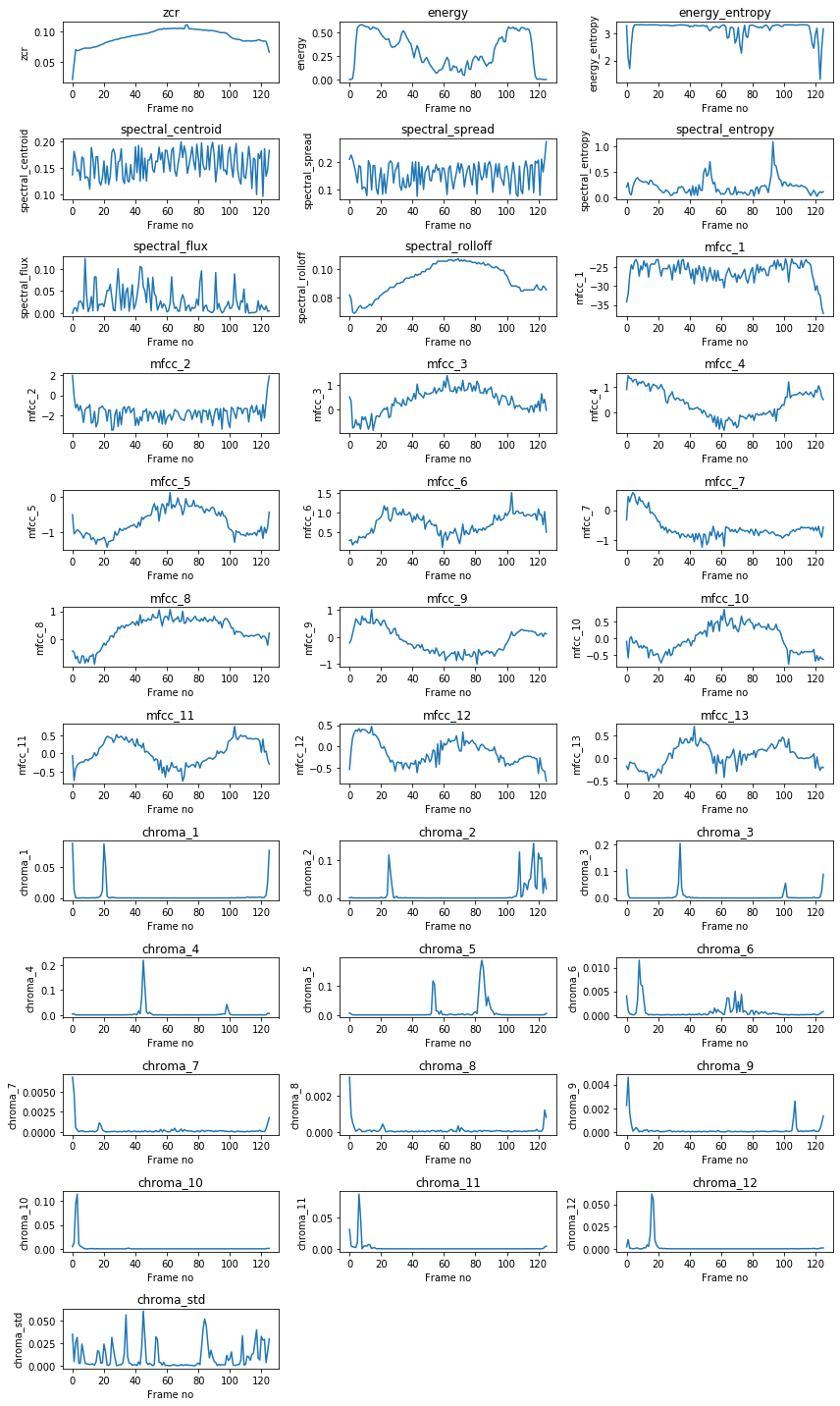
plt.rcParams['figure.figsize'] = [12, 20]
for num,val in enumerate(f_names):
plt.subplot(math.ceil(len(f_names)/3),3,num+1); plt.plot(F[num,:])
plt.xlabel('Frame no')
plt.title(val)
plt.ylabel(val)
plt.tight_layout();
# Que tipo de dato es el resultado
type(F)
numpy.ndarray
F.shape
(34, 126)
Grabar Resultados
import pandas as pd
df = pd.DataFrame(F) #convertir matriz numpy en Dataframe
df.index = f_names # agregar el nombre de cada caracteristica
df = df.T # transponer el dataframe, Features como columnas
df.head()
| zcr | energy | energy_entropy | spectral_centroid | spectral_spread | spectral_entropy | spectral_flux | spectral_rolloff | mfcc_1 | mfcc_2 | ... | chroma_4 | chroma_5 | chroma_6 | chroma_7 | chroma_8 | chroma_9 | chroma_10 | chroma_11 | chroma_12 | chroma_std | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.020417 | 0.000010 | 3.286130 | 0.137610 | 0.209820 | 0.201767 | 0.000000 | 0.081670 | -34.175493 | 1.968927 | ... | 0.004005 | 0.006756 | 0.004017 | 0.006802 | 0.003048 | 0.002235 | 0.004689 | 0.031335 | 0.002253 | 0.035113 |
| 1 | 0.046733 | 0.000053 | 2.091771 | 0.182037 | 0.225613 | 0.287889 | 0.011477 | 0.078947 | -32.105190 | -0.076838 | ... | 0.003757 | 0.003051 | 0.000989 | 0.004848 | 0.000957 | 0.004627 | 0.013178 | 0.005021 | 0.010425 | 0.004640 |
| 2 | 0.069873 | 0.011794 | 1.702007 | 0.167220 | 0.209679 | 0.080099 | 0.012601 | 0.069873 | -27.188918 | -1.237966 | ... | 0.000228 | 0.000204 | 0.000233 | 0.000511 | 0.000508 | 0.001604 | 0.093217 | 0.003182 | 0.000651 | 0.025575 |
| 3 | 0.068512 | 0.131178 | 2.570339 | 0.144510 | 0.185425 | 0.048914 | 0.004301 | 0.068966 | -24.404932 | -0.888496 | ... | 0.000123 | 0.000127 | 0.000138 | 0.000262 | 0.000259 | 0.000669 | 0.115040 | 0.002734 | 0.000570 | 0.031670 |
| 4 | 0.068966 | 0.385592 | 3.164735 | 0.147036 | 0.158561 | 0.207502 | 0.025614 | 0.069873 | -25.507026 | -1.520837 | ... | 0.000019 | 0.000108 | 0.000020 | 0.000025 | 0.000031 | 0.000064 | 0.010057 | 0.002052 | 0.000118 | 0.002773 |
5 rows × 34 columns
# Grabar la informacion a un archivo
df.to_csv('Low_Term-Features.csv',header = True, index = False)
# Leer el archivo grabado
df2 = pd.read_csv('Low_Term-Features.csv')
df2.head()
| zcr | energy | energy_entropy | spectral_centroid | spectral_spread | spectral_entropy | spectral_flux | spectral_rolloff | mfcc_1 | mfcc_2 | ... | chroma_4 | chroma_5 | chroma_6 | chroma_7 | chroma_8 | chroma_9 | chroma_10 | chroma_11 | chroma_12 | chroma_std | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.020417 | 0.000010 | 3.286130 | 0.137610 | 0.209820 | 0.201767 | 0.000000 | 0.081670 | -34.175493 | 1.968927 | ... | 0.004005 | 0.006756 | 0.004017 | 0.006802 | 0.003048 | 0.002235 | 0.004689 | 0.031335 | 0.002253 | 0.035113 |
| 1 | 0.046733 | 0.000053 | 2.091771 | 0.182037 | 0.225613 | 0.287889 | 0.011477 | 0.078947 | -32.105190 | -0.076838 | ... | 0.003757 | 0.003051 | 0.000989 | 0.004848 | 0.000957 | 0.004627 | 0.013178 | 0.005021 | 0.010425 | 0.004640 |
| 2 | 0.069873 | 0.011794 | 1.702007 | 0.167220 | 0.209679 | 0.080099 | 0.012601 | 0.069873 | -27.188918 | -1.237966 | ... | 0.000228 | 0.000204 | 0.000233 | 0.000511 | 0.000508 | 0.001604 | 0.093217 | 0.003182 | 0.000651 | 0.025575 |
| 3 | 0.068512 | 0.131178 | 2.570339 | 0.144510 | 0.185425 | 0.048914 | 0.004301 | 0.068966 | -24.404932 | -0.888496 | ... | 0.000123 | 0.000127 | 0.000138 | 0.000262 | 0.000259 | 0.000669 | 0.115040 | 0.002734 | 0.000570 | 0.031670 |
| 4 | 0.068966 | 0.385592 | 3.164735 | 0.147036 | 0.158561 | 0.207502 | 0.025614 | 0.069873 | -25.507026 | -1.520837 | ... | 0.000019 | 0.000108 | 0.000020 | 0.000025 | 0.000031 | 0.000064 | 0.010057 | 0.002052 | 0.000118 | 0.002773 |
5 rows × 34 columns
Ahora lo que falta realizar estadistica descriptiva de las low-term features para poder realizar aplicaciones de:
- Prediccion
- Clasificacion
- Agrupamiento (clusterizacion)
Libreria Essentia
Essentia es una libreria de código abierto escrito en c++ para mayor velocidad y brinda herramientas para análisis de audio y música, descripción y síntesis. Esta libreria se puede instalar y usar desde Python.
Estos son algunas de las caracteristicas que se pueden extraer:
- Statistical descriptors: median, mean, variance, power means, raw and central moments, spread, kurtosis, skewness, flatness
- Time-domain descriptors: duration, loudness, LARM, Leq, Vickers’ loudness, zero-crossing-rate, log attack time and other signal envelope descriptors
- Spectral descriptors: Bark/Mel/ERB bands, MFCC, GFCC, LPC, spectral peaks, complexity, rolloff, contrast, HFC, inharmonicity and dissonance
- Tonal descriptors: Pitch salience function, predominant melody and pitch, HPCP (chroma) related features, chords, key and scale, tuning frequency
- Rhythm descriptors: beat detection, BPM, onset detection, rhythm transform, beat loudness
- Other high-level descriptors: danceability, dynamic complexity, audio segmentation, SVM classifier
Puedes ver un tutorial en python en este link
# cargar libreria
import essentia
import essentia.standard
import matplotlib.pyplot as plt
import pandas as pd
# Todos los Metodos en essentia standard
dir(essentia.standard)
loader = essentia.standard.MonoLoader(filename='./Data/Whistle.wav')
audio = loader()
plt.rcParams['figure.figsize'] = (15, 6) # set plot sizes to something larger than default
plt.plot(audio)
plt.title("Forma de Onda");
Essentia tiene archivos ejecutables que extraen automaticamente todas las caracteristicas de un archivo de audio, no es necesario realizar instalaciones, solo descargarlo y usarlo, estos programas funcionan es en linea de comando. Esta para Windows /Linux / Mac OS (Os X) -> http://essentia.upf.edu/documentation/extractors/
El listado de todas las caracteristicas se pueden ver en este link
essentia_streaming_extractor_music: calcula un amplio conjunto de descriptores espectrales, del dominio de tiempo, de ritmo, tonales y de alto nivel. Los descriptores por segmentos se resumen por su distribución estadística y se pueden producir opcionalmente por segmentos. Este extractor fue diseñado para extraerlas caraccteristicas en grandes colecciones de música y es la forma más sencilla de sacar el máximo provecho de descriptores de música de Essentia sin programación.
#Descargar en google colab
# Ejecutar el programa desde linea de comando
# la salida es un archivo JSON
# en Jupyter se pueden ejecutar comandos agregando al principio !
# En linux y google Colab
!./streaming_extractor_music ./Data/Whistle.wav features_essentia.json
# En windows
#!streaming_extractor_music.exe ./Data/Whistle.wav features_essentia.json
Leer caracteristicas extraidas
df_audio = pd.read_json('features_essentia.json')
df_audio.head()
| lowlevel | metadata | rhythm | tonal | |
|---|---|---|---|---|
| average_loudness | 0.98189 | NaN | NaN | NaN |
| barkbands_crest | {'dmean': 1.4540450573, 'dmean2': 2.1039736270... | NaN | NaN | NaN |
| barkbands_flatness_db | {'dmean': 0.045052662491800004, 'dmean2': 0.06... | NaN | NaN | NaN |
| barkbands_kurtosis | {'dmean': 583.721557617, 'dmean2': 850.4887695... | NaN | NaN | NaN |
| barkbands_skewness | {'dmean': 5.6545443534899995, 'dmean2': 8.4234... | NaN | NaN | NaN |
df_audio.index.name = 'features' # agregar el nombre feature a los index
df_audio.head()
| lowlevel | metadata | rhythm | tonal | |
|---|---|---|---|---|
| features | ||||
| average_loudness | 0.98189 | NaN | NaN | NaN |
| barkbands_crest | {'dmean': 1.4540450573, 'dmean2': 2.1039736270... | NaN | NaN | NaN |
| barkbands_flatness_db | {'dmean': 0.045052662491800004, 'dmean2': 0.06... | NaN | NaN | NaN |
| barkbands_kurtosis | {'dmean': 583.721557617, 'dmean2': 850.4887695... | NaN | NaN | NaN |
| barkbands_skewness | {'dmean': 5.6545443534899995, 'dmean2': 8.4234... | NaN | NaN | NaN |
# Cuales caracteristicas tengo
df_audio.index
Index(['average_loudness', 'barkbands_crest', 'barkbands_flatness_db',
'barkbands_kurtosis', 'barkbands_skewness', 'barkbands_spread',
'dissonance', 'dynamic_complexity', 'erbbands_crest',
'erbbands_flatness_db', 'erbbands_kurtosis', 'erbbands_skewness',
'erbbands_spread', 'hfc', 'melbands_crest', 'melbands_flatness_db',
'melbands_kurtosis', 'melbands_skewness', 'melbands_spread',
'pitch_salience', 'silence_rate_20dB', 'silence_rate_30dB',
'silence_rate_60dB', 'spectral_centroid', 'spectral_complexity',
'spectral_decrease', 'spectral_energy', 'spectral_energyband_high',
'spectral_energyband_low', 'spectral_energyband_middle_high',
'spectral_energyband_middle_low', 'spectral_entropy', 'spectral_flux',
'spectral_kurtosis', 'spectral_rms', 'spectral_rolloff',
'spectral_skewness', 'spectral_spread', 'spectral_strongpeak',
'zerocrossingrate', 'barkbands', 'erbbands', 'gfcc', 'melbands', 'mfcc',
'spectral_contrast_coeffs', 'spectral_contrast_valleys',
'audio_properties', 'tags', 'version', 'beats_count', 'beats_loudness',
'bpm', 'bpm_histogram_first_peak_bpm',
'bpm_histogram_first_peak_spread', 'bpm_histogram_first_peak_weight',
'bpm_histogram_second_peak_bpm', 'bpm_histogram_second_peak_spread',
'bpm_histogram_second_peak_weight', 'danceability', 'onset_rate',
'beats_loudness_band_ratio', 'beats_position', 'chords_changes_rate',
'chords_number_rate', 'chords_strength', 'hpcp_entropy', 'key_strength',
'tuning_diatonic_strength', 'tuning_equal_tempered_deviation',
'tuning_frequency', 'tuning_nontempered_energy_ratio', 'hpcp',
'chords_histogram', 'thpcp', 'chords_key', 'chords_scale', 'key_key',
'key_scale'],
dtype='object', name='features')
# Algunas son estadisticas
df_audio.loc['spectral_energy']['lowlevel']
{'dmean': 0.00385777838528,
'dmean2': 0.00590370735154,
'dvar': 1.478568538e-05,
'dvar2': 3.12479060085e-05,
'max': 0.0423069857061,
'mean': 0.0212880317122,
'median': 0.020806664601,
'min': 1.76752945613e-10,
'var': 0.000196065229829}
# Otras son el vectores con las estadisticas por bandas
df_audio.loc['erbbands']['lowlevel']
df_audio
| lowlevel | metadata | rhythm | tonal | |
|---|---|---|---|---|
| features | ||||
| average_loudness | 0.98189 | NaN | NaN | NaN |
| barkbands_crest | {'dmean': 1.4540450573, 'dmean2': 2.1039736270... | NaN | NaN | NaN |
| barkbands_flatness_db | {'dmean': 0.045052662491800004, 'dmean2': 0.06... | NaN | NaN | NaN |
| barkbands_kurtosis | {'dmean': 583.721557617, 'dmean2': 850.4887695... | NaN | NaN | NaN |
| barkbands_skewness | {'dmean': 5.6545443534899995, 'dmean2': 8.4234... | NaN | NaN | NaN |
| ... | ... | ... | ... | ... |
| thpcp | NaN | NaN | NaN | [1, 0.5622935891149999, 0.0647645443678, 0.011... |
| chords_key | NaN | NaN | NaN | C# |
| chords_scale | NaN | NaN | NaN | minor |
| key_key | NaN | NaN | NaN | F# |
| key_scale | NaN | NaN | NaN | major |
79 rows × 4 columns
Phd. Jose R. Zapata
