Señal de Audio en el Tiempo
#Importar Modulo scipy para leer y grabar audio
from scipy.io import wavfile
import numpy as np
import IPython.display as ipd
AudioName = "Whistle.wav" # Archivo de Audio
# Salida fs: Frecuencia de muestreo and data: Señal de audio -> int16
fs, Audiodata = wavfile.read(AudioName)
print(f'Duracion = {Audiodata.shape[0]/fs} , Frecuencia de Muestreo = {fs} [=] Muestras/Seg' \
f', Wav format = {Audiodata.dtype}')
ipd.Audio(AudioName) # Reproduce el audio directamente en el Jupyter notebook.
Duracion = 3.1887981859410433 , Frecuencia de Muestreo = 44100 [=] Muestras/Seg, Wav format = int16
import matplotlib.pyplot as plt #Libreria para realizar graficos
plt.rcParams['figure.figsize'] = (15, 5) # Definir el tamaño de graficas
# Definir los valores de los datos de amplitud entre [-1 : 1] Audiodata.dtype es int16
AudiodataScaled = Audiodata / (2.**15)
#definir los valores del eje x en milisegundos
timeValues = np.arange(0, len(AudiodataScaled), 1)/ fs # Convertir Muestras/Seg a Segundos
timeValues = timeValues * 1000 #Escala de tiempo en milisegundos
# importar la libreria plotly offline para graficar
import plotly.offline as pyo # realizar graficas offline
from plotly.offline import init_notebook_mode #para poder graficar dentro del jupyter notebook
import plotly.graph_objs as go
init_notebook_mode() # inicializar el uso de plotly dentro del jupyter notebook
datos = [go.Scatter(x = timeValues,y = AudiodataScaled,mode = 'lines')]
layout = go.Layout(title = 'Señal de Audio',xaxis = dict(title = 'Tiempo (ms)'),yaxis = dict(title = 'Amplitud'))
fig = go.Figure(data=datos,layout=layout)
pyo.iplot(fig, filename='Audio')
Estadistica descriptiva
La señal de audio es una serie de tiempo de como cambiar la presion, ¿Como son estadisticamente los datos de una señal de audio?
AudioName = "oboe_c6.wav" # Archivo de Audio
# Salida fs: Frecuencia de muestreo and data: Señal de audio -> int16
fs, Audiodata = wavfile.read(AudioName)
Audiodata = Audiodata / (2.**15) #convertirla entre [-1,1]
timeValues = np.arange(0, len(Audiodata), 1)/ fs # Convertir Muestras/Seg a Segundos
timeValues = timeValues * 1000
print(f'Frecuencia de Muestreo = {fs} [=] Muestras/Seg, Numero de datos: {len(Audiodata)}')
Frecuencia de Muestreo = 22050 [=] Muestras/Seg, Numero de datos: 23625
datos1 = [go.Scatter(x = timeValues,y = Audiodata,mode = 'lines')]
fig = go.Figure(data=datos1,layout=layout)
pyo.iplot(fig, filename='Audio1')
ipd.Audio(AudioName)
Descripcion Estadistica de los datos
import pandas as pd # convertir arreglo numpy en una serie de pandas
X = pd.Series(Audiodata)
X.describe()
count 23625.000000
mean -0.000889
std 0.392807
min -0.867279
25% -0.244995
50% 0.000000
75% 0.311157
max 0.999969
dtype: float64
print('Varianza = {}'.format( X.var())) # Varianza
print('Desviacion Standard = {}'.format( X.std())) # Desviacion estandard
print('Skewnesss = {}'.format( X.skew())) # Skewness
print('Kurtosis = {}'.format( X.kurt())) # Kurtosis
Varianza = 0.15429766584730864
Desviacion Standard = 0.3928074157234161
Skewnesss = -0.11488179650378598
Kurtosis = -0.6859091306828673
# Histograma y densidad
import plotly.figure_factory as ff
hist_data = [X]
group_labels = ['Oboe']
fig = ff.create_distplot(hist_data, group_labels,bin_size=0.01,show_rug=False)
fig['layout'].update(title='Histograma y KDE Señal de Audio')
pyo.iplot(fig, filename='Basic Distplot')
trace0 = [go.Box(y=X, name = 'Oboe')] # Boxplot
fig = go.Figure(data=trace0)
fig['layout'].update(title='Boxplot Señal de Audio')
pyo.iplot(fig, filename='Grafica-boxplot')
Si se comparan varios audios: ¿seran diferentes?
fs1, Audiodata1 = wavfile.read('oboe_c6.wav')
Audiodata1 = Audiodata1 / (2.**15)
ipd.display(ipd.Audio('oboe_c6.wav'))
fs2, Audiodata2 = wavfile.read('clarinet_c6.wav')
Audiodata2 = Audiodata2 / (2.**15)
ipd.display(ipd.Audio('clarinet_c6.wav'))
fs3, Audiodata3 = wavfile.read('Whistle.wav')
Audiodata3 = Audiodata3 / (2.**15)
ipd.display(ipd.Audio('Whistle.wav'))
# Graficar las formas de onda
plt.rcParams['figure.figsize'] = (15, 5) # Definir el tamaño de graficas
for n in range(3):
pos = n+1
plt.subplot(3,1,pos) # posición de la grafica
nombre_variable = vars()['Audiodata'+str(pos)] #convertir string a nombre de variable
plt.plot(nombre_variable); #graficar cada forma de onda
plt.tight_layout()
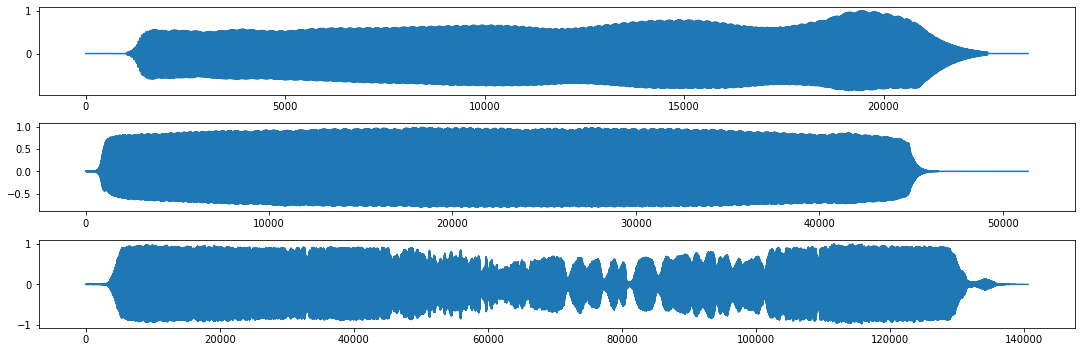
df = pd.DataFrame([Audiodata1,Audiodata2,Audiodata3]).T
print(f'frecuencias de muestreo de los archivos: fs1 = {fs1}, fs2 = {fs2} y fs3 = {fs3}')
print('Tamaño del data frame = {}'.format( df.shape)) # Tamaño del dataframe
print('Duracion en Segundos = {}'.format(len(df)/fs3)) # numero_de_datos / fs = tiempo
frecuencias de muestreo de los archivos: fs1 = 22050, fs2 = 22050 y fs3 = 44100
Tamaño del data frame = (140626, 3)
Duracion en Segundos = 3.1887981859410433
140626 datos !!!!
Si es monofonico como de 3 segundos¿Por que tantos?
¿Entonces el audio tiene muchos datos? -> SI
#df.plot.box(title = 'Boxplot de las señales de audio');
Oboe = go.Box(y=df[0], name = 'Oboe');
Clarinete = go.Box(y=df[1], name = 'Clarinete');Whistle = go.Box(y=df[2], name = 'Whistle')
datos = [Oboe, Clarinete,Whistle]
fig = go.Figure(data=datos);
fig['layout'].update(title='Boxplot Señales de Audio')
pyo.iplot(fig, filename='Grafica-boxplot2')
Descripcion Estadistica de los datos
df.describe() # Descripcion Estadistica general de los datos
| 0 | 1 | 2 | |
|---|---|---|---|
| count | 23625.000000 | 51386.000000 | 140626.000000 |
| mean | -0.000889 | -0.000206 | -0.000015 |
| std | 0.392807 | 0.481685 | 0.546089 |
| min | -0.867279 | -0.803619 | -0.976196 |
| 25% | -0.244995 | -0.424194 | -0.470825 |
| 50% | 0.000000 | 0.000000 | -0.000275 |
| 75% | 0.311157 | 0.384056 | 0.458733 |
| max | 0.999969 | 0.986176 | 0.998260 |
Correlacion de los datos
# Correlation Matrix
import numpy as np # se deben rotar los datos 90 grados
data = ff.create_annotated_heatmap( z=np.rot90((np.array(df.corr()))),
x = ['Whistle','Clarinete','Oboe'],
y= ['Oboe', 'Clarinete','Whistle'])
pyo.iplot(data, filename='corr-heatmap')
pero la correlacion muestra que son muy diferentes
¿Que Caracteristicas se extraen del Audio para Utilizarlo en Ciencia de datos?
Phd. Jose R. Zapata
